Capteurs et objectifs
Cette note correspond à la Section 6.4 du Guide de Ressources en Imagerie.
Imagerie à la fréquence de Nyquist
Il peut être tentant de prendre des images à ce que l'on appelle la fréquence de Nyquist, qui est définie dans l'équation 1 de la section Le choix d’un objectif d’imagerie - considérations plus poussées. Cependant, ce n'est généralement pas une bonne idée, car cela implique que la caractéristique observée se trouve sur un seul pixel. Si le système d'imagerie se décalait d'un demi-pixel, l'objet d'intérêt se situerait entre deux pixels et serait complètement flou. Pour cette raison, il n'est pas recommandé de prendre des images à la fréquence de Nyquist. En supposant qu'aucune interpolation sous-pixel n'est utilisée, il est généralement recommandé de prendre des images à la moitié de la fréquence de Nyquist, car cela permet à l'élément d'intérêt de toujours occuper au moins deux pixels.
Une autre hypothèse, souvent erronée, est qu'un objectif n'est pas adapté à une caméra particulière s'il ne présente pas un contraste important (>20%) à la fréquence de Nyquist du capteur avec lequel il est utilisé. Ce n'est pas le cas. Comme nous l'avons mentionné précédemment, l'imagerie à la limite de Nyquist est peu judicieux et peut créer plusieurs problèmes. Il faut examiner l'ensemble du système pour déterminer si un objectif est approprié ou non pour un capteur de caméra donné, et cela dépend souvent de l'application. La section suivante décrit ce qui se passe dans un système d'imagerie lorsqu'ils sont utilisés à ou près de la fréquence de Nyquist, et les conséquences sur la résolution globale du système.
Comprendre l'interaction entre les capteurs de caméra et les objectifs d'imagerie est un élément essentiel de la conception et de la mise en œuvre d'un système de vision industrielle. L'optimisation de cette relation est souvent négligée et l'impact qu'elle peut avoir sur la résolution globale du système est important. Une combinaison caméra/objectif mal adaptée peut également entraîner des coûts inutiles pour le système d’imagerie. Malheureusement, il n'est pas toujours facile de déterminer l'objectif et la caméra à utiliser dans une application donnée : de plus en plus de capteurs de caméra (et, par conséquent, de plus en plus d'objectifs) continuent d'être conçus et fabriqués pour tirer parti des nouvelles capacités de fabrication et améliorer les performances. Ces nouveaux capteurs présentent un certain nombre de défis à relever pour les objectifs et rendent moins évidente l'association correcte d'une caméra et d'un objectif.
Le premier défi est que les pixels continuent de se réduire. Si des pixels plus petits signifient généralement une résolution plus élevée au niveau du système, ce n'est pas toujours le cas une fois que l'on tient compte de l'optique utilisée. Dans un monde parfait, sans diffraction ni erreurs optiques dans un système, la résolution serait simplement basée sur la taille d'un pixel et la taille de l'objet visualisé (voir Résolution). Pour résumer brièvement, plus la taille des pixels diminue, plus la résolution augmente. Cette augmentation est due au fait qu'il est possible de placer des objets plus petits sur des pixels plus petits tout en étant capable de résoudre l'espacement entre les objets, même si cet espacement diminue. Il s'agit d'un modèle simplifié à l'extrême de la manière dont le capteur d'une caméra détecte les objets, sans tenir compte du bruit ou d'autres paramètres.
Les objectifs ont également des spécifications de résolution, mais les bases ne sont pas aussi faciles à comprendre que les capteurs, car il n'y a rien d'aussi concret qu'un pixel. Cependant, deux facteurs déterminent en fin de compte la reproduction du contraste (fonction de transfert de modulation, ou FTM) d'une caractéristique particulière d'un objet sur un pixel lorsqu'il est imagé à travers un objectif : la diffraction et le contenu aberrant. La diffraction se produit chaque fois que la lumière passe par une ouverture, ce qui entraîne une réduction du contraste (pour plus de détails, voir La tache d'Airy et la limite de diffraction). Les aberrations sont des erreurs qui se produisent dans chaque objectif d'imagerie et qui brouillent ou déplacent les informations de l'image en fonction du type d'aberration, comme décrit dans la section Real World Performance. Avec un objectif rapide (≤f/4), les aberrations optiques sont le plus souvent la cause d'un système qui s'écarte de la « perfection » telle qu'elle serait dictée par la limite de diffraction ; dans la plupart des cas, les objectifs ne fonctionnent tout simplement pas à leur fréquence de coupure théorique ($ \small{\xi_{\small{\text{Cutoff}}}} $ ), comme le dicte l'équation 1.
Pour ramener cette équation au capteur d'une caméra, plus la fréquence des pixels augmente (la taille des pixels diminue), plus le contraste diminue - chaque objectif suivra toujours cette tendance. Cependant, cela ne tient pas compte des performances matérielles réelles d'un objectif. Le degré de tolérance et de fabrication d'un objectif aura également un impact sur le contenu d’aberration d'un objectif et les performances réelles seront différentes des performances nominales, telles que conçues. Il peut être difficile d'estimer les performances d'un objectif réel à partir de données nominales, mais les tests en laboratoire peuvent aider à déterminer si un objectif particulier et le capteur d'une caméra sont compatibles.
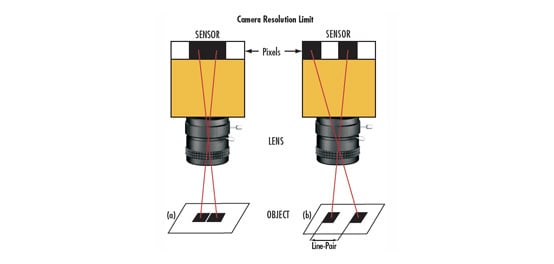
Une façon de comprendre comment un objectif se comportera avec un certain capteur est de tester sa résolution avec une mire de barres USAF 1951. Les mires de barres permettent de mieux déterminer la compatibilité lentille/capteur que les mires étoilées, car leurs caractéristiques correspondent mieux aux pixels carrés (et rectangulaires). Les exemples suivants montrent des images de test prises avec le même objectif haute résolution de distance focale 50 mm et les mêmes conditions d'éclairage sur trois capteurs de caméra différents. Chaque image est ensuite comparée à la courbe FTM nominale, sur l'axe, de l'objectif (courbe bleue). Seule la courbe sur l'axe est utilisée dans ce cas car la région d'intérêt où le contraste a été mesuré ne couvrait qu'une petite partie du centre du capteur. La Figure 1a montre les performances de l'objectif de 50 mm lorsqu'il est associé à un 1/2,5” ON Semiconductor MT9P031 avec des pixels de 2,2 µm, à un grossissement de 0,177X.

Figure 1 : La comparaison des performances nominales de l'objectif par rapport aux performances réelles pour un objectif haute résolution de 50 mm sur le (a) ON Semiconductor MT9P031 avec des pixels de 2,2 μm, le (b) Sony IXC655 avec des pixels de 3,45 μm et le (c) ON Semiconductor KAI-4021 avec des pixels de 7,4 μm. Les lignes rouge, violette et vert foncé montrent les limites de Nyquist des capteurs, respectivement. Les lignes jaune, bleu clair et vert clair indiquent la moitié des limites de Nyquist des capteurs, respectivement.
En utilisant l'équation 1 de Résolution, la résolution de Nyquist du capteur ($\xi_{\small{\text{Sensor}}}$) est de 227,7$ \small{ \tfrac{\text{lp}}{\text{mm}}} $, ce qui signifie que le plus petit objet que le système pourrait théoriquement imager avec un grossissement de 0,177X est de 12,4 µm (en utilisant une autre forme de l'équation 1 de Résolution).
Gardez à l'esprit que ces calculs ne sont associés à aucune valeur de contraste. La partie gauche de la Figure 1a montre les images de deux éléments sur une mire 'USAF 1951 ; l'image de gauche montre deux pixels par élément, et l'image de droite montre un pixel par élément. A la fréquence de Nyquist du capteur (227$ \small{ \tfrac{\text{lp}}{\text{mm}}} $), le système image la mire avec un contraste de 8,8%, ce qui est inférieur au contraste minimum de 20% recommandé pour un système d'imagerie fiable. Notez qu'en augmentant la taille des caractéristiques d'un facteur deux à 24,8 μm, le contraste est augmenté de près d'un facteur trois. D'un point de vue pratique, le système d'imagerie serait beaucoup plus fiable à la moitié de la fréquence de Nyquist.
La conclusion selon laquelle le système d'imagerie n'a pas été en mesure d'obtenir une image fiable d'un objet d'une taille de 12,4 µm est en contradiction directe avec ce que montrent les équations de la section Résolution, puisque mathématiquement les objets sont dans les limites des capacités du système. Cette contradiction souligne que les calculs et les approximations du premier ordre ne suffisent pas à déterminer si un système d'imagerie peut ou non atteindre une résolution particulière. En outre, le calcul de la fréquence de Nyquist n'est pas une mesure solide sur laquelle on peut s'appuyer pour déterminer les capacités de résolution d'un système et ne doit être utilisé qu'à titre indicatif pour déterminer les limites d'un système. Un contraste de 8,8% est trop faible pour être considéré comme précis, car des fluctuations mineures des conditions pourraient facilement faire baisser le contraste à des niveaux impossibles à résoudre.
Les Figures 1b et 1c montrent des images similaires à celles du MT9P031 bien que les capteurs utilisés soient le Sony ICX655 (pixels de 3,45 µm) et le ON Semiconductor KAI-4021 (pixels de 7,4 µm). Les images de gauche dans chaque figure montrent deux pixels par caractéristique et les images de droite montrent un pixel par caractéristique. La principale différence entre les 3 figures est que tous les contrastes d'image des figures 1b et 1c sont supérieurs à 20%, ce qui signifie (à première vue) qu'ils seraient fiables pour résoudre des caractéristiques de cette taille. Bien entendu, les objets de taille minimale qu'ils peuvent résoudre sont plus grands que les pixels de 2,2 µm de la Figure 1a. Cependant, l’imagerie à la fréquence de Nyquist est toujours déconseillée, car de légers mouvements de l'objet pourraient déplacer la caractéristique souhaitée entre deux pixels, rendant l'objet impossible à résoudre. Notez que lorsque la taille des pixels augmente de 2,2 µm, à 3,45 µm, à 7,4 µm, les augmentations respectives du contraste d'un pixel par caractéristique à deux pixels par caractéristique ont moins d'impact. Sur l'ICX655 (pixels de 3,45 µm), le contraste change d'un peu moins d'un facteur 2 ; cet effet est encore plus réduit avec le KAI-4021 (pixels de 7,4 µm).

Figure 2 : Images prises avec le même objectif et dans les mêmes conditions d'éclairage sur trois capteurs de caméra différents avec trois tailles de pixel différentes. Les images en haut sont prises avec quatre pixels par caractéristique, et les images en bas sont prises avec deux pixels par caractéristique.
Un écart important dans la Figure 1 est la différence entre la FTM nominale de l'objectif et le contraste réel dans une image réelle. La courbe FTM de l’objectif en haut de la Figure 1a montre que l’objectif devrait atteindre un contraste d'environ 24% à la fréquence de 227l$ \small{ \tfrac{\text{lp}}{\text{mm}}} $, alors que la valeur de contraste produite était de 8,8%. Deux facteurs principaux contribuent à cette différence : la FTM du capteur et les tolérances de l'objectif. La plupart des fabricants de capteurs ne publient pas de courbes FTM pour leurs capteurs, mais elles ont la même forme générale que celle de l'objectif. La FTM au niveau du système étant un produit des FTM de tous les composants d'un système, les FTM de l'objectif et du capteur doivent être multipliées ensemble pour fournir une conclusion plus précise sur les capacités de résolution globales d'un système.
Comme mentionné ci-dessus, une FTM tolérancée d'un objectif est également un écart par rapport à la valeur nominale. Tous ces facteurs se combinent pour modifier la résolution attendue d'un système et, à elle seule, la courbe FTM d'un objectif n'est pas une représentation précise de la résolution au niveau du système.
Comme le montrent les images de la Figure 2, le meilleur contraste au niveau du système se trouve dans les images prises avec les pixels les plus grands. Lorsque la taille des pixels diminue, le contraste baisse considérablement. Une bonne pratique consiste à utiliser 20% comme contraste minimum dans un système de vision industrielle, car toute valeur de contraste inférieure est trop sensible aux fluctuations du bruit provenant des variations de température ou de la diaphonie de l'éclairage. L'image prise avec l'objectif de 50 mm et le pixel de 2,2 µm de la Figure 1a présente un contraste de 8,8% et est trop faible pour que l'on puisse se fier aux données de l'image pour les tailles des caractéristiques des objets correspondant à la taille du pixel de 2,2 µm, car l'objectif est sur le point de devenir le facteur limitant du système. Les capteurs dont les pixels sont beaucoup plus petits que 2,2 µm existent certainement et sont assez populaires, mais en dessous de cette taille, il est presque impossible pour l'optique de résoudre le problème au niveau du pixel individuel. Cela signifie que les équations décrites dans la section Résolution n'ont plus aucun sens sur le plan fonctionnel pour aider à déterminer la résolution au niveau du système, et que des images similaires à celles prises dans les figures susmentionnées seraient impossibles à saisir. Toutefois, ces minuscules pixels ont encore une utilité : ce n'est pas parce que l'optique ne peut pas résoudre la totalité du pixel qu'elle est inutile. Pour certains algorithmes, tels que l'analyse de blob ou la reconnaissance optique de caractères (OCR), il s'agit moins de savoir si l'objectif peut effectivement résoudre jusqu'au niveau du pixel individuel que de savoir combien de pixels peuvent être placés sur une caractéristique particulière. Avec des pixels plus petits, l'interpolation sous-pixel peut être évitée, ce qui ajoute à la précision de toute mesure effectuée avec elle. En outre, la perte de résolution est moins importante lorsque l'on passe à une caméra couleur équipée d'un filtre de Bayer.
Un autre point important à retenir est que le passage d'un pixel par caractéristique à deux pixels par caractéristique permet de récupérer une quantité substantielle de contraste, en particulier sur les plus petits pixels. Bien qu'en divisant la fréquence par deux, l'objet minimal résoluble double effectivement de taille. S'il est absolument nécessaire de visualiser jusqu'au niveau du pixel, il est souvent préférable de doubler le grossissement de l'optique et de réduire de moitié le champ de vision (FOV).
Ainsi, la taille de l'élément couvrira deux fois plus de pixels et le contraste sera beaucoup plus élevé. L'inconvénient de cette solution est qu'une partie moins importante du champ global sera visible. Du point de vue du capteur d'image, la meilleure chose à faire est de maintenir la taille des pixels et de doubler la taille du format du capteur d'image. Par exemple, un système d'imagerie avec un grossissement 1X utilisant un capteur ½" avec un pixel de 2,2 µm aura le même champ de vision et la même résolution spatiale qu'un système avec un grossissement 2X utilisant un capteur 1" avec un pixel de 2,2 µm, mais avec le système 2X, le contraste est théoriquement doublé.
Malheureusement, le fait de doubler la taille du capteur crée des problèmes supplémentaires pour les objectifs. L'un des principaux facteurs de coût d'un objectif d'imagerie est la taille du format pour lequel il a été conçu. La conception d'un objectif pour un capteur de plus grand format nécessite un plus grand nombre de composants optiques individuels ; ces composants doivent être plus grands et les tolérances du système doivent être plus serrées. En poursuivant l'exemple ci-dessus, un objectif conçu pour un capteur de 1" peut coûter cinq fois plus cher qu'un objectif conçu pour un capteur de ½", même s'il ne peut pas atteindre les mêmes spécifications de résolution limitée en pixels.













 Section précédente
Section précédente




















































































































































ou consulter les numéros d’autres pays
facile à utiliser
entrer les numéros de stock pour commencer
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
L'entreprise Edmund Optics GmbH en Allemagne agit comme un mandataire d'Edmund Optics Ltd au Royaume-Uni. Le titulaire du contrat est Edmund Optics Ltd au Royaume-Uni.