Résolution
Auteurs : Gregory Hollows, Nicholas James
Cette note correspond à la Section 2.2 du Guide de Ressources en Imagerie.
La résolution est la capacité d'un système d'imagerie à reproduire les détails d'un objet. Elle peut être influencée par des facteurs tels que le type d'éclairage utilisé, la taille des pixels du capteur et les capacités de l'optique. Plus les détails de l'objet sont petits, plus la résolution requise est élevée.
Si l'on divise le nombre de pixels horizontaux ou verticaux d'un capteur par la taille de l'objet que l'on souhaite observer, on obtient l'espace que chaque pixel couvre sur l'objet et on peut l'utiliser pour estimer la résolution. Cependant, cela ne permet pas de déterminer réellement si les informations du pixel peuvent être distinguées de celles de tout autre pixel.
Il est important de comprendre ce qui peut limiter la résolution du système. La Figure 1 montre une paire de carrés sur un fond blanc. Si les carrés sont représentés sur des pixels voisins du capteur de la caméra, ils apparaîtront comme un rectangle plus grand (a), plutôt que comme deux carrés séparés (b). Pour distinguer les carrés, il faut qu'au moins un pixel les sépare. Cette distance minimale est la résolution limite du système. La limite absolue est définie par la taille des pixels sur le capteur et le nombre de pixels sur le capteur.

Figure 1 : Résolution de deux carrés. Si l'espace entre les carrés est trop petit (a), le capteur de la caméra sera incapable de les résoudre comme des objets distincts.
La paire de lignes et les limites du capteur
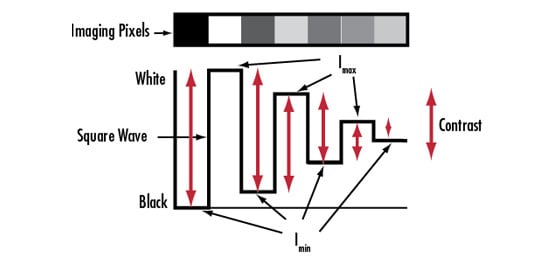
La résolution est souvent présentée comme une dimension. Ce concept de résolution comme étant la taille minimale qui peut être résolue par un objectif ou un système n'est pas une description complète de la résolution. La résolution est plus précisément décrite comme une fréquence, mesurée en paires de lignes par millimètre $ \left[ \small{\tfrac{\text{lp}}{\text{mm}}} \right] $. Une paire de lignes est une paire de carrés noirs et blancs dans l'espace objet. La résolution des objectifs n'est malheureusement pas absolue. À une résolution donnée, la capacité de voir les deux carrés comme des entités distinctes dépendra du niveau de gris. Un système peut plus facilement résoudre une paire de lignes si la différence entre les niveaux de gris des carrés et de l'espace entre eux est plus grande (Figure 1b). Cette différence de niveau de gris est appelée contraste. La résolution est donc définie comme une fréquence spatiale, donnée en $ \left[ \small{\tfrac{\text{lp}}{\text{mm}}} \right] $, à laquelle un contraste spécifique est atteint.
Le contraste est fixé par convention pour les différents fabricants d'objectifs et de caméras, mais il est généralement spécifié pour les objectifs à 20%. C'est pourquoi le calcul de la résolution en termes de $ \left[ \small{\tfrac{\text{lp}}{\text{mm}}} \right] $ est extrêmement utile pour comparer les objectifs et déterminer le meilleur choix pour des capteurs et des applications donnés (pour plus d'informations, lisez la section Contraste).
Le capteur est le point de départ du calcul de la résolution du système. En commençant par le capteur, il est plus facile de déterminer les performances de l'objectif nécessaires pour répondre aux exigences du capteur ou d'autres applications. La fréquence la plus élevée pouvant être résolue par un capteur, la fréquence de Nyquist, correspond effectivement à deux pixels ou à une paire de lignes. Le Tableau 1 montre la limite de Nyquist associée aux tailles de pixel que l'on trouve sur certains capteurs courants. La résolution du capteur $ \left( \xi _{\small{\text{Capteur}}} \right) $, appelée résolution de l'espace image du système $ \left( \xi _{\small{\text{Espace image}}} \right) $, est calculée en multipliant la taille du pixel(s), généralement exprimée en µm, par 2 (pour créer une paire), puis en divisant ce résultat par 1000 pour le convertir en mm :
Les capteurs dont les pixels sont plus grands auront des résolutions limites plus faibles. Les capteurs dont les pixels sont plus petits auront des résolutions limites plus élevées. La manière dont ces informations sont utilisées pour déterminer les performances nécessaires de l'objectif est présentée dans la section sur les performances et limites du capteur. La résolution limite sur l'objet à visualiser peut être calculée en utilisant les relations entre la taille du capteur, le champ de vision (FOV) et le nombre de pixels sur le capteur.
La taille du capteur fait référence à la taille de la zone active du capteur d'une caméra, spécifiée par la taille du format du capteur (vous trouverez de plus amples informations sur le format du capteur dans la section Capteurs). Toutefois, les proportions exactes du capteur varient en fonction du rapport d’aspect, de sorte que les formats nominaux des capteurs ne doivent être utilisés qu'à titre indicatif, notamment pour les objectifs télécentriques et les objectifs à fort grossissement. La taille du capteur (H), horizontale, verticale ou diagonale, peut être directement calculée à partir de la taille des pixels et du nombre de pixels actifs sur le capteur(p).
| Taille du pixel (µm) | Limite de Nyquist associée $ \left( \tfrac{\text{lp}}{\text{mm}} \right) $ |
|---|---|
| 1,67 | 299,4 |
| 2,2 | 227,3 |
| 3,45 | 144,9 |
| 4,54 | 110,1 |
| 5,5 | 90,9 |
Tableau 1 : Lorsque la taille du pixel augmente, la limite de Nyquist associée dans $ \left[ \small{\tfrac{\text{lp}}{\text{mm}}} \right] $ diminue proportionnellement.
Résolution de l’espace objet
Pour déterminer le point résoluble minimum absolu visible sur l'objet, il faut calculer le rapport entre le FOV et la taille du capteur. C'est ce qu'on appelle également le grossissement du système
Le grossissement du système met à l'échelle la résolution de l'espace image jusqu'à la résolution de l'espace objet $ \left( \xi _{\small{\text{Espace objet}}} \right) $.
Lors du développement d'une application, la résolution de l'espace objet d'un système est généralement spécifiée en tant que dimension de longueur, plutôt qu'en $ \left[ \small{\tfrac{\text{lp}}{\text{mm}}} \right] $. Il y a deux façons d'effectuer cette conversion :
Bien qu'il soit facile de sauter à la résolution limite sur l'objet en utilisant la dernière formule, il est très utile de déterminer la résolution et le grossissement de l'espace d'imagerie pour simplifier le choix de l'objectif. Il est également important de noter que de nombreux facteurs supplémentaires entrent en jeu, et que cette limite est souvent bien inférieure à ce qui peut être facilement calculé à l'aide des équations. Pour en savoir plus sur les limites du contraste et le choix de l’objectif, consultez les sections Contraste et Types of Machine Vision Lenses.
Exemples de calcul de la résolution et du grossissement avec un capteur Sony ICX625
Paramètres connus :
Taille des pixels : 3,45 × 3,45 μm
Nombre de pixels : 2448 × 2050
FOV souhaité (horizontal) : 100 mm
Limitation de la résolution du capteur:
\begin{align} \xi_{\small{\text{Espace image}}} & = \left( \frac{1}{2 \times s} \right) \times \left( \frac{1000 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}}}{1 \text{mm}} \right) \\ & = \left( \frac{1}{2 \times 3,45 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}}} \right) \times \left( \frac{1000 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}}}{1 \text{mm}} \right) \approx 145 \tfrac{\text{lp}}{ \text{mm}} \end{align}
Dimensions du capteur:
$$ H_{\small{\text{horizontal}}} = 3,45 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} \times 2448 \times \left( \frac{1 \text{mm}}{1000 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}}} \right) = 8,45 \text{mm} $$
$$ H_{\small{\text{vertical}}} = 3,45 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} \times 2050 \times \left( \frac{1 \text{mm}}{1000 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}}} \right) = 7,07 \text{mm} $$
Grossissement :
$$ m = \frac{8,56 \text{mm}}{100 \text{mm}} = 0,0845X $$
Résolution:
$$ \xi_{\small{\text{Espace objet}}} \left[ \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} \right] = 145 \tfrac{\text{lp}}{\text{mm}} \times 0,0845 = 12,25 \tfrac{\text{lp}}{\text{mm}} \approx 41 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} $$













 Section précédente
Section précédente






































































































































































































ou consulter les numéros d’autres pays
facile à utiliser
entrer les numéros de stock pour commencer
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
L'entreprise Edmund Optics GmbH en Allemagne agit comme un mandataire d'Edmund Optics Ltd au Royaume-Uni. Le titulaire du contrat est Edmund Optics Ltd au Royaume-Uni.