Dispersion
Cela correspond à la section 8.8 du Guide des Ressources en Optique Laser.
La dispersion est la dépendance de la vitesse de phase ou du retard de phase de la lumière lorsqu’elle est transmise à travers un milieu optique, à un autre paramètre, comme la fréquence optique ou la longueur d’onde. Plusieurs types de dispersion peuvent se produire à l’intérieur du substrat d’une optique : dispersion chromatique (Figure 1), intermodale et de mode de polarisation.1
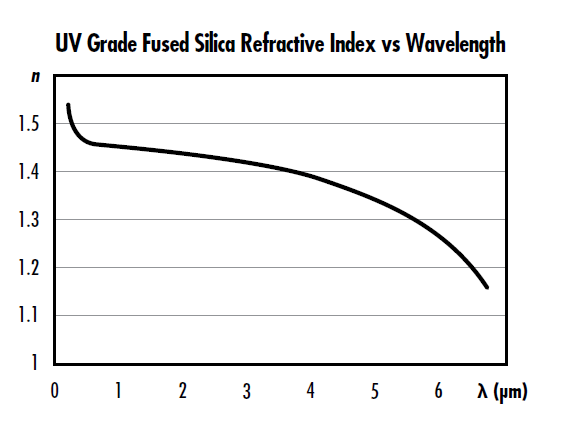
Figure 1 : Indice de réfraction de la silice fondue indice UV en fonction de la longueur d’onde
Dispersion chromatique
L’indice de réfraction est le rapport entre la vitesse de la lumière dans le vide et la vitesse de phase d’une onde lumineuse lorsqu’elle traverse un milieu, tel que l’air ou le verre. Dans les applications de laser pulsé, la lumière est généralement décrite à l’aide de la fréquence car le temps est généralement plus critique et la fréquence de la lumière est une valeur fixe, alors que sa longueur d’onde dépend de l’indice de réfraction dans lequel elle se déplace. La longueur d’onde $ \small{\left( \lambda \right)} $ est liée à la fréquence angulaire $ \small{\left( \omega \right)} $, à l’indice de réfraction $ \small{\left( n \right)} $ et à la vitesse de la lumière $ \small{\left( c \right)} $ par :
L’indice de réfraction d’un matériau est souvent décrit à l’aide de la formule de Sellmeier et des constantes matérielles $\small{B_1}$, $\small{B_2}$, $\small{B_3}$, $\small{C_1}$, $\small{C_2}$, et $\small{C_3}$:
La dispersion chromatique est une dépendance de la vitesse de phase de la lumière $\small{\nu _{p}}$ dans un milieu à sa longueur d’onde, résultant principalement de l’interaction de la lumière avec les électrons du milieu. La dispersion chromatique est décrite par le nombre d’Abbe (Figure 2), qui correspond à la réciproque de la dérivée première partielle de l’indice de réfraction par rapport à $ \small{\lambda} $, et la dispersion partielle, qui correspond à la dérivée seconde de l’indice de réfraction par rapport à la longueur d’onde.
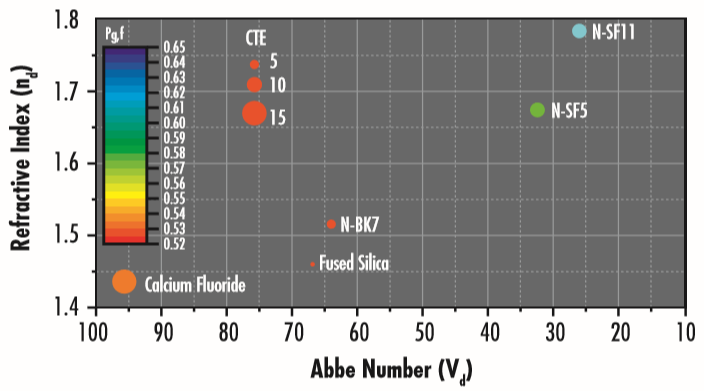
Figure 2 : Diagramme d’Abbe montrant l’indice de réfraction des types de verre courants en fonction de leur nombre d’Abbe Le CTE (coefficient de dilatation thermique) est défini dans la note d’application Propriétés thermiques des substrats optiques.
Le nombre d’Abbe est donné par :
$\small{n_D} $, $\small{n_F} $, et $\small{n_C} $ asont les indices de réfraction du substrat aux longueurs d’onde des raies spectrales D- $ \small{\left( 589, \!3 \text{nm} \right)} $, F- $ \small{\left( 486, \! 1 \text{nm} \right)} $ et C- $ \small{\left( 656, \! 3 \text{nm} \right)} $ de Fraunhofer. Le nombre d’Abbe d’un matériau peut également être décrit à n’importe quelle longueur d’onde en utilisant la dérivée de l’indice de réfraction par rapport à la longueur d’onde :
Dans les applications laser, la principale préoccupation est de savoir comment la dispersion affectera les propriétés d’une impulsion laser se déplaçant à travers le milieu, qui est décrit par la vitesse de groupe - la variation de la vitesse de phase de la lumière dans un milieu par rapport à son nombre d’onde :
Le nombre d’onde $ \small{\left( k \right)} $ est $ \tfrac{2 \pi}{\lambda} $ ; ce concept est parfois aussi désigné par le terme de phase spectrale. Lorsque plusieurs longueurs d’onde de lumière traversent un matériau, la plus grande longueur d’onde (fréquence inférieure) se déplace généralement plus vite que les longueurs d’onde plus courtes (fréquences supérieures), car la vitesse du groupe dépend de la longueur d’onde.2 Il en résulte un étalement spectral de la phase du front d’onde similaire à la façon dont la lumière traversant un prisme est dispersée pour donner les couleurs qui le composent. La vitesse de groupe est définie comme la dérivée première de la vitesse de phase par rapport à la fréquence, et la dispersion de vitesse de groupe (ou $ \small{\text{GVD}} $ pour Group Velocity Dispersion) est définie de façon similaire comme la dérivée de la vitesse de groupe inverse par rapport à la fréquence :
La vitesse de groupe est similaire à la dispersion spectrale, car toutes deux correspondent à la dérivée première de l’indice de réfraction par rapport à la longueur d’onde ou à la fréquence. De même, la dispersion de vitesse de groupe est similaire à la dispersion partielle dans la mesure où elles correspondent toutes deux à la dérivée seconde par rapport à la longueur d’onde ou à la fréquence. La minimisation de la $ \small{\text{GVD}} $ dans une conception optique est similaire à la conception visant à minimiser le décalage focal chromatique, sauf que le concepteur se concentrera sur la vitesse de groupe et la $ \small{\text{GVD}} $ plutôt que sur le nombre d’Abbe et la dispersion partielle.
Vous trouverez une discussion plus approfondie sur la $ \small{\text{GVD}} $ et son importance pour l’optique laser ultrarapide dans notre note d’application Dispersion ultrarapide.
Dispersion intermodale
La dispersion intermodale est une dépendance de la vitesse de groupe de la lumière dans un guide d’onde, comme une fibre multimode, à la fréquence optique et au mode de propagation.2 Dans les systèmes de communication par fibre optique multimode, le débit de transmission de données, ou débit binaire, qu’il est possible d’atteindre est fortement réduit. La dispersion intermodale pourrait être évitée en utilisant des fibres monomodes ou des fibres multimodes avec un profil d’indice de réfraction parabolique.
Dispersion de mode de polarisation
La dispersion de mode de polarisation est la dépendance des caractéristiques de propagation de la lumière dans un milieu par rapport à l’état de polarisation, ce qui peut être pertinent dans les systèmes à fibre monomode à haut débit. Ces trois types de dispersion peuvent entraîner un élargissement ou une compression temporelle des impulsions ultracourtes dans l’espace libre ou dans les fibres optiques, ce qui peut provoquer le mélange d’impulsions séparées et les rendre méconnaissables (Figure 3).
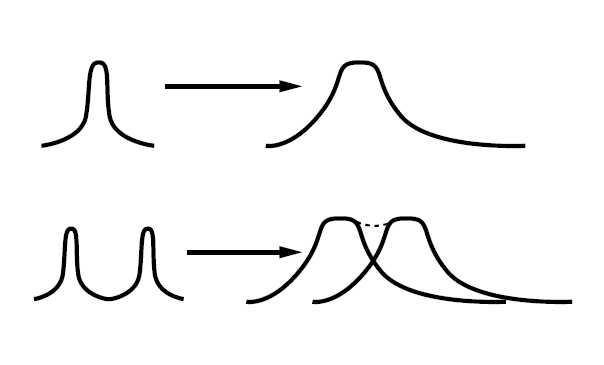
Figure 3 : La dispersion peut entraîner la dispersion des impulsions laser qui parcourent les fibres jusqu’à ce qu’elles deviennent méconnaissables
Références
1 Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
2 Ghatak, Ajoy, and K. Thyagarajan. “Optical Waveguides and Fibers.” University of Connecticut, 2000.
More Resources
- Ultrafast Dispersion
- Wavelength Effects on Performance
- Chromatic and Monochromatic Optical Aberrations
- Why Use an Achromatic Lens?
- "An achromat singlet" by Joel Bagwell, Christian Hebert, and Nathan Carlie - SPIE
- Absorption
- Optical Glass
- Thermal Properties of Optical Substrates
- Homogeneity and Scatter from Inclusions and Bubbles
- Subsurface Damage
- Common Laser Optics Materials
- Laser Optics Lab Video Series













 Section précédente
Section précédente 













ou consulter les numéros d’autres pays
facile à utiliser
entrer les numéros de stock pour commencer
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
POLITIQUE DE CONFIDENTIALITÉ | POLITIQUE DE COOKIES | CONDITIONS GÉNÈRALES | CONDITIONS GÉNÈRALES B2C | MENTIONS LÉGALES | ACCESSIBILITÉ
L'entreprise Edmund Optics GmbH en Allemagne agit comme un mandataire d'Edmund Optics BV aux Pays-Bas.
Le titulaire du contrat est Edmund Optics BV aux Pays-Bas.
The FUTURE Depends On Optics®