Dispersion ultrarapide

Tandis que l’effet de la dispersion est minime pour de nombreux types de systèmes laser, il s’avère particulièrement problématique dans les applications laser ultrarapides. Les lasers ultrarapides sont caractérisés par des durées d’impulsion très courtes, de l’ordre de la picoseconde, de la femtoseconde ou de l’attoseconde. En raison du principe d’incertitude de Heisenberg, les impulsions ultrarapides transformées de Fourier atteignant la limite inférieure de leur durée d’impulsion ont une large bande passante de longueurs d’ondes (Figure 1). Alors que la transmission de ces impulsions de large bande passante a lieu à travers des milieux optiques, la dispersion chromatique prolonge la durée d’impulsion, ce qui s’avère préjudiciable pour les applications ultrarapides.

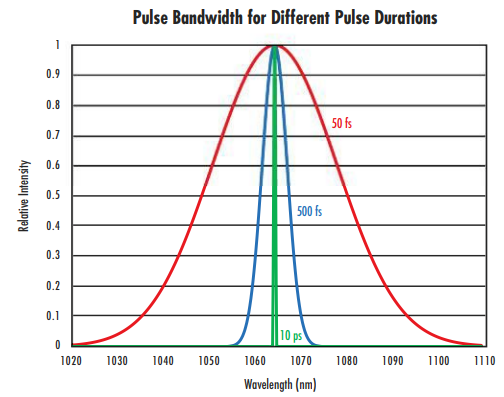
Figure 1 : Tandis que la durée d’impulsion d’un laser ultrarapide diminue, la bande passante de longueur d’onde augmente

Aperçu de la dispersion chromatique

La manière dont une impulsion laser se propage à travers un milieu optique se traduit par la vitesse de groupe $ \small{v_g}$ – la variation de la vitesse de phase de la lumière dans un milieu par rapport à son nombre d’onde $ \small{k}$ :

(1)$$ v_g = \left( \frac{\partial k}{\partial \omega} \right)^{-1} = c \left[ \frac{\partial}{\partial \omega} \left( \omega n \! \left( \omega \right) \right) \right] ^{-1} = \frac{c}{n \! \left( \omega \right) + \omega \frac{\partial n}{\partial \omega}} = \frac{c}{n_g \! \left( \omega \right)} $$

$ \small{\omega}$ correspond à la fréquence angulaire de la lumière, $ \small{c} $ à la vitesse de la lumière dans le vide et  $ \small{n} $  à l’indice de réfraction du milieu. Le nombre d’onde $ \small{k}$ correspond à $ \tfrac{2 \pi}{\lambda}$ ; ce concept est parfois désigné comme fréquence spatiale de l’onde. La différence entre la vitesse de phase et la vitesse de groupe est illustrée dans la Figure 2.

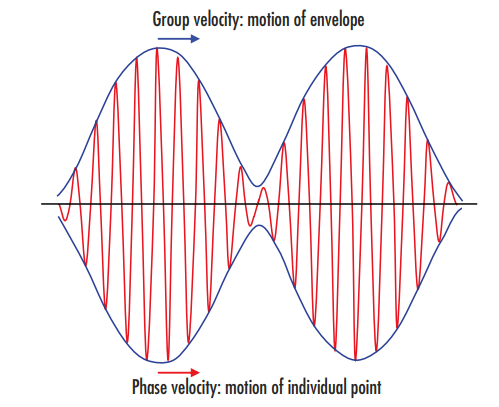
Figure 2 : La vitesse de groupe définit le mouvement de l’enveloppe, ou paquet d’onde, illustré en bleu, tandis que la vitesse de phase définit le mouvement de fréquence supérieure de chaque point individuel de l’onde elle-même, illustré en rouge

Lorsque la lumière de plusieurs longueurs d’onde se propage à travers un matériau, il est fréquent que la longueur d’onde plus longue (basses fréquences) se propage sensiblement plus rapidement que les longueurs d’onde plus courtes en raison d’une dépendance de fréquence (ou de longueur d’onde) de la vitesse de groupe.¹ Cela entraîne une variation spectrale de la phase du front d’onde, de la même manière que la lumière se propageant à travers un prisme se divise en couleurs composantes à partir de la dispersion spectrale du matériau. Puisque la vitesse de groupe est donnée comme dérivée première de la vitesse de phase en termes de fréquence, la dispersion de vitesse de groupe (ou $ \small{ \text{GVD}} $ pour Group Velocity Dispersion) est la dérivée de la vitesse de groupe inverse en termes de fréquence :

(2)$$ \text{GVD} = \frac{\partial}{\partial \omega} \left( \frac{1}{v_g} \right) = \frac{\partial}{\partial \omega} \left( \frac{\partial k}{ \partial \omega} \right) = \frac{\partial ^2 k}{\partial \omega ^2} $$

La vitesse de groupe inverse est appelée dispersion de premier ordre et la $ \small{ \text{GVD}} $ est appelée dispersion de second ordre. De même que la vitesse de groupe est similaire à la dispersion spectrale dans la mesure où les deux correspondent à la dérivée première de l’indice de réfraction en termes de longueur d’onde ou de fréquence, la $ \small{ \text{GVD}} $ est utilisée de manière similaire à la dispersion partielle étant donné que les deux sont des dérivées secondes en termes de longueur d’onde ou de fréquence. La conception de composants optiques pour $ \small{ \text{GVD}} $ faible s’apparente à la conception ciblant des performances chromatiques élevées, mis à part le fait que l’accent est mis sur la vitesse de groupe et la $ \small{ \text{GVD}} $  plutôt que sur le nombre d’Abbe et la dispersion partielle associés.

La $ \small{ \text{GVD}} $ est indépendante de la longueur du milieu optique donné. La dispersion des retards de groupe (ou $ \small{ \text{GDD}} $ pour Group Delay Dispersion) considère la longueur du milieu et peut être obtenue en multipliant la $ \small{ \text{GVD}} $par la longueur.

(3)$$ \text{GDD} = \text{GVD} \times \text{Longueur} $$

La $ \small{ \text{GVD}} $dépend fortement de la longueur d’onde et est typiquement exprimée en $ \tfrac{\text{fs}^2}{\text{mm}} $. Par exemple, la $ \small{ \text{GVD}} $ de silice fondue est de $ \small{+} 57 \tfrac{\text{fs}^2}{\text{mm}} $ á 589.3 nm et de $ \small{−} 26 \tfrac{\text{fs}^2}{\text{mm}} $ á 1500 nm. À un certain niveau entre ces deux longueurs d’onde (à environ 1,3 μm) se trouve une longueur d’onde à dispersion nulle où la $ \small{ \text{GVD}} $ est de zéro. La Figure 3 illustre le degré de variation significatif de la $ \small{ \text{GVD}} $ de silice fondue comparée à la longueur d’onde. Dans le cadre des communications par fibre optique, la $ \small{ \text{GVD}} $ est généralement définie comme la dérivée en termes de longueur d’onde plutôt que de fréquence et est le plus souvent spécifiée en unités de $ \tfrac{\text{ps}}{\text{nm km}} $.

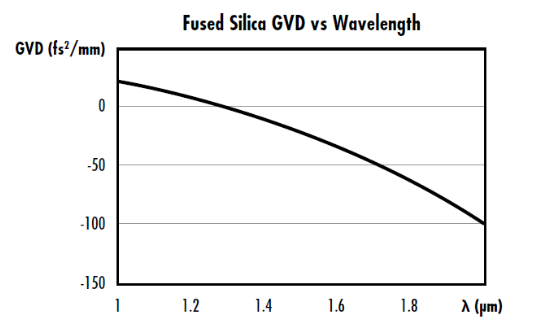
Figure 3 : Comparaison de la GVD et de la longueur d’onde pour la silice fondue avec une longueur d’onde de dispersion nulle aux environs de 1,3 μm

Lasers ultrarapides

Les lasers ultrarapides sont extrêmement avantageux en raison de leurs courtes durées d’impulsion et de leurs puissances élevées pour une grande diversité d’applications notamment les applications médicales de haute précision, le traitement de matériaux, le micro-usinage, l’imagerie et la microscopie non linéaires et les communications. Les lasers ultrarapides permettent d’obtenir de meilleures tolérances dimensionnelles dans le cadre du traitement de matériaux et du micro-usinage tout en éliminant les étapes usuelles post-traitement et en minimisant les dommages occasionnés au niveau des surfaces environnantes.² De la même manière, les lasers ultrarapides permettent de minimiser les chocs dans le cadre de la chirurgie laser et d’autres applications médicales, réduisant également les besoins en anesthésie et en stérilisation.³ Les impulsions laser ultrarapides sont créées lorsque les ondes lumineuses contenant une grande quantité de modes, ou des multiples entiers de la moitié de la longueur d’onde de la lumière, sont émises de manière cohérente par leur superposition en phase (Figure 4). On appelle également cela « verrouillage de mode.

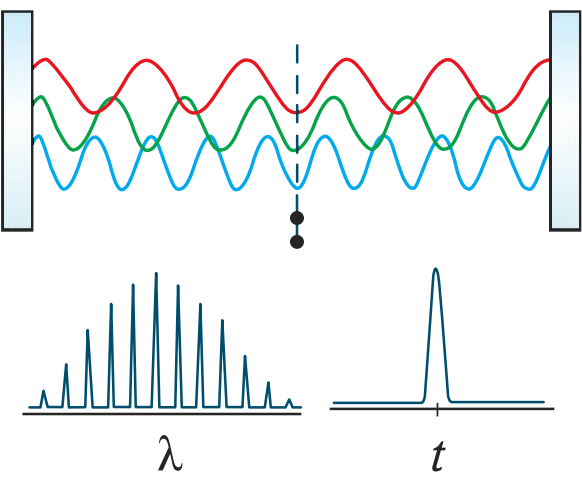
Figure 4 : L’interférence d’ondes cohérentes avec de nombreux modes au cours du verrouillage de mode génère des impulsions avec une largeur temporelle ultrarapide mais une large bande passante de longueur d’onde

Le fait que la $ \small{ \text{GVD}} $ dépende de la longueur d’onde impacte de manière significative les impulsions ultrarapides en raison de leur large bande passante, prolongeant la durée d’impulsion des impulsions ultrarapides pendant qu’elles se propagent à travers un système optique (Figure 5). Le degré d’extension d’impulsion de la durée d’impulsion incidente (τ_In) à la durée d’impulsion de sortie (τ_Out) est relatif à la $ \small{ \text{GDD}} $ (Figure 6):

(4)$$ \tau_{\tiny{\text{Out}}}= \tau_{\tiny{\text{In}}} \sqrt{1 + \left( \frac{4 \ln{\left( 2 \times \text{GDD} \right)} }{\tau_{\tiny{\text{In}}} ^2} \right)^2} $$

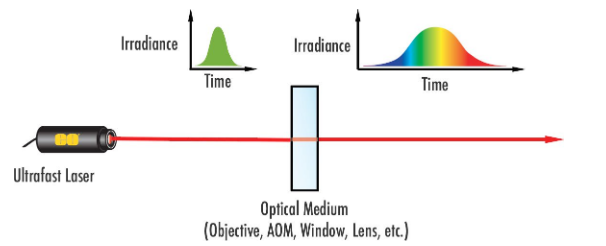
Figure 5 : La dispersion entraîne l’extension d’impulsions laser ultrarapides. L’acronyme MAO désigne un modulateur acousto-optique, composant permettant aux lasers d’émettre une sortie pulsée

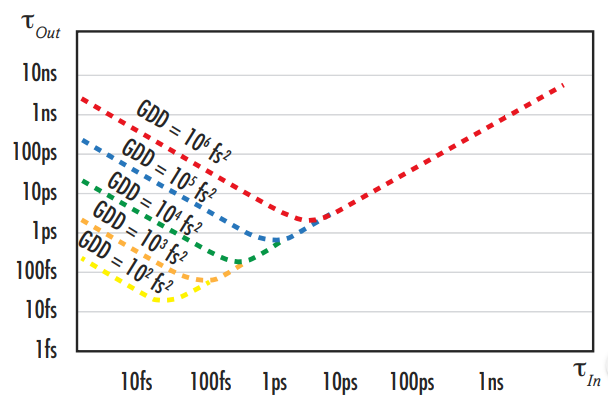
Figure 6 : Illustration de l’extension temporelle ou prolongation de la durée d’impulsion d’une impulsion ultrarapide de l’ordre de la femtoseconde s’étant propagée à travers différents milieux optiques

La plupart des milieux optiques montrent une dispersion positive, de sorte que les longueurs d’onde plus longues les traversant montrent une vitesse de phase supérieure par rapport à des longueurs d’onde plus courtes, prolongeant la durée d’impulsion (Figure 5). On appelle cela « fluctuation de fréquence positive ». Les lasers ultrarapides sont beaucoup plus impactés par la dispersion que les autres types de laser en raison de leur large bande passante.

L’interférométrie de lumière blanche constitue le type de métrologie le plus communément utilisé pour mesurer le retard de groupe et la $ \small{ \text{GVD}} $ pour les composants optiques ultrarapides. Vous trouverez de plus amples informations dans notre note d’application Miroirs hautement dispersifs.

Outre l’élargissement d’impulsion, la dispersion chromatique risque également de produire des angles de réfraction sur des surfaces optiques dépendants de la fréquence, provoquant une dispersion angulaire et des longueurs de trajet optiques dépendantes de la fréquence. Des méthodes de compensation de dispersion permettant d’améliorer les performances de systèmes laser ultrarapides sont décrites dans notre Note d’application : Miroirs hautement dispersifs.

Références:

1. Ghatak, Ajoy, and K. Thyagarajan. “Optical Waveguides and Fibers.” University of Connecticut, 2000.
2. Mielke, Michael. “Ultrafast Lasers: Ultrashort Pulse Lasers Bring Cost-Efficient Precision to Micromanufacturing.” Laser Focus World, 8 Apr. 2015.
3. “The Benefits of Femtosecond Lasers and Why We Use Them.” Spindel Eye Associates, 16 May 2017, www.spindeleye.com/blog/2017/05/the-benefits-of-femtosecond-lasers-and-why-we-use-them/.

Section précédente Section suivante