LIDT pour lasers ultrarapides

Les lasers ultrarapides sont des lasers pulsés à mode bloqué qui émettent des impulsions de durée extrêmement courte (de l’ordre de la femtoseconde ou de la picoseconde) et de forte puissance de pointe. En raison de la limite de Fourier, ou incertitude énergie-temps, des longueurs d’impulsion temporelles plus courtes correspondent à des écarts importants dans le spectre des longueurs d’onde. Ainsi, les impulsions ultrarapides présentent une bande passante de longueur d’onde plus large que les impulsions plus longues (Figure 1). Les lasers ultrarapides sont avantageux dans de nombreuses applications, notamment la physique de haute intensité, le traitement femtoseconde des matériaux et la spectroscopie laser.¹

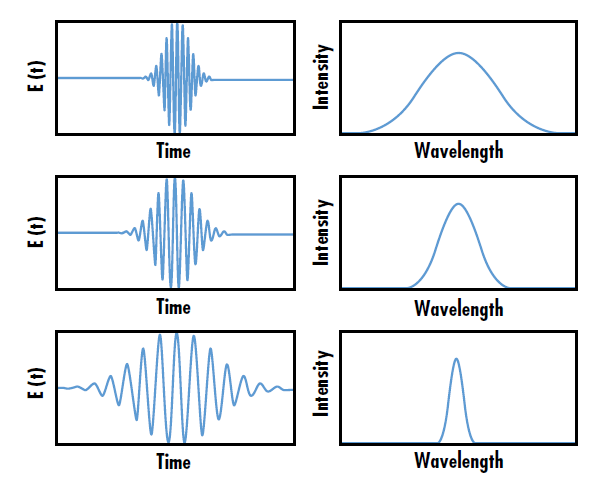
Figure 1 : La bande passante de longueur d’onde des impulsions laser ultrarapides est inversement proportionnelle au temps par impulsion

Ces dernières années, les dommages causés par les lasers ultrarapides ont fait l’objet de nombreuses recherches car la durée d’impulsion extrêmement brève des lasers ultrarapides amène ces derniers à interagir différemment avec les traitements et composants optiques, comparés aux autres lasers pulsés. En général, l’échauffement des traitements à couche mince après une exposition aux lasers ultrarapides résulte d’un transport d’énergie hors équilibre. L’énergie des photons incidents est absorbée par les électrons à l’état fondamental, ce qui conduit à une occupation des états d’énergie excités en quelques femtosecondes. Ces électrons dits « chauds » perdent leur excitation pour revenir à leur état fondamental grâce à la diffusion phonon-électron et phonon-phonon à l’échelle de la picoseconde, ce qui permet une redistribution de l’énergie dans les matériaux de traitement.^{2, 3} La diffusion phonon-électron décrit les distorsions des fonctions d’ondes électroniques causées par les vibrations du réseau, tandis que la diffusion phonon-phonon décrit les vibrations du réseau induisant d’autres vibrations dans le réseau (Figure 2).

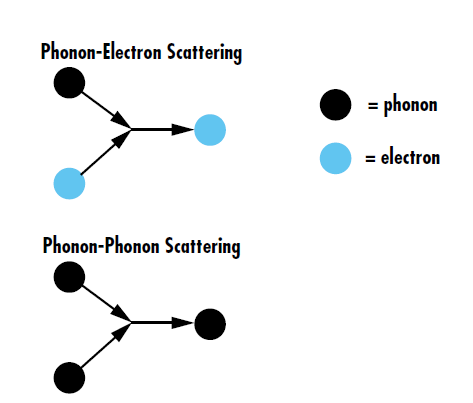
Figure 2 : La diffusion phonon-électron est le transfert d’énergie entre les vibrations du réseau et les électrons, les électrons étant redirigés à l’intérieur du réseau, tandis que la diffusion phonon-phonon est l’interaction de multiples vibrations du réseau créant de nouveaux phonons

Comme la distribution de Fermi des électrons est beaucoup plus rapide que la redistribution du réseau électronique, la couche mince peut être décrite comme une composition de deux sous-systèmes en interaction : les électrons et les phonons.⁴ Il est essentiel de connaître l’augmentation de température causée par une excitation ultra-rapide pour comprendre le LIDT pour les lasers ultrarapides. La dynamique de relaxation du porteur chaud peut faire l’objet d’un calcul théorique et d’une vérification expérimentale à l’aide de la spectroscopie pompe-sonde ultrarapide qui mesure les changements des propriétés optiques de l’optique de test en fonction du temps.^{5, 6}

Le comportement thermique de l’électron et du réseau sous excitation laser ultrarapide peut être décrit en utilisant un modèle à deux températures qui suppose que les sous-systèmes de l’électron et du réseau atteignent indépendamment et spontanément l’équilibre. Les équations de capacité thermique couplées, utilisées pour déterminer l’augmentation théorique de la température à partir d’une excitation ultrarapide, s’expriment comme suit⁷ :

• C_e et C_l sont les capacités thermiques pour les sous-systèmes de l’électron et du réseau
• T_e et T_l sont les températures de l’électron et du réseau
• k_e est la conductivité thermique de l’électron
• S est un terme de réchauffement introduit par l’impulsion laser ultrarapide dépendant du temps (t) et de l’espace (z)
• G est la constante de couplage du réseau électronique exprimée comme suit :

• m_e est la masse effective de l’électron
• n_e est la densité du nombre d’électrons
• c_s est la vitesse du son dans le matériau en vrac, décrite comme étant la racine carrée du rapport du module d’élasticité volumique sur la densité ρ_m
• τ(T_e) est le temps de relaxation des électrons

Les Équations 1, Equation 2, et 3 servent à donner T_l et T_e en fonction du temps. La Figure 3 montre les valeurs théoriques de T_l et T_e calculées pour une impulsion laser ultrarapide de 0.2 J/cm² 10 fs centrée à 800 nm avec un diamètre de faisceau de 120 μm éclairant un nanofilm d’or de 200 nm d’épaisseur en suspension sur un substrat de cuivre. L’épaisseur du nanofilm d’or est beaucoup plus élevée que la profondeur de pénétration optique et électronique dans le nanofilm.

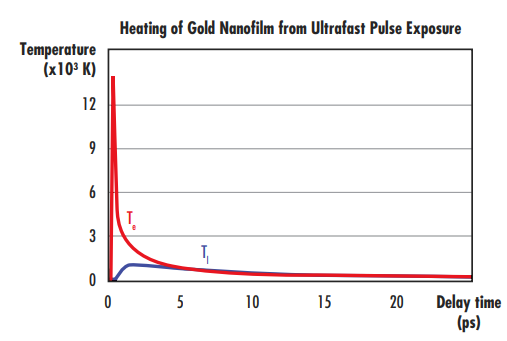
Figure 3 : Augmentation de la température des électrons (rouge) et du réseau (bleu) en fonction du temps, suite à l’excitation par un laser ultrarapide d’une impulsion laser ultrarapide de 0.2 J/cm² 10 fs centrée à 800 nm. L’échauffement du nanofilm d’or dû à l’augmentation de la température du réseau donne lieu aux dommages causés par le laser

La température des électrons atteint rapidement des températures extrêmement élevées (13 000 K). Les processus d’équilibrage du réseau électronique entraînent alors une augmentation de la température du réseau (T_l), laquelle atteint des valeurs d’environ 1 300. T_l est du même ordre que la température de fusion de l’or (1337 K) ; en raison de cette impulsion ultrarapide relativement faible avec une fluence de seulement 0.2 J/cm² le réseau a atteint le point de fusion de l’or.

Le système de non-équilibre dissipe son énergie par diffusion électron-phonon et phonon-phonon et un transfert d’énergie retardé du nanofilm d’or vers le substrat de cuivre environnant fournit un canal de dissipation d’énergie supplémentaire. L’augmentation de la température du réseau atteint des niveaux remarquablement élevés, ce qui peut entraîner des dommages induits par le laser dans le film de traitement. Il est indispensable de comprendre la rethermalisation ultrarapide qui suit l’excitation laser pour concevoir et optimiser les traitements optiques pour les applications laser ultrarapides.

L’impact théorique des impulsions ultrarapides peut être vérifié de manière expérimentale par la spectroscopie pompe-sonde ultrarapide, comme la diffraction ultrarapide des électrons. Un faisceau de pompe ultrarapide est utilisé pour exciter l’échantillon d’essai, tandis qu’un faisceau de sonde de faible puissance surveille les changements d’intensité des électrons diffractés de l’échantillon causés par l’état de non-équilibre (Figure 4). La variation de l’intensité de la diffraction des électrons en fonction du délai entre l’arrivée des impulsions dans les faisceaux de la pompe et de la sonde révèle la dynamique du réseau électronique.⁸ Une telle dynamique montre les voies de relaxation des électrons excités qui conduisent au chauffage du nanofilm.

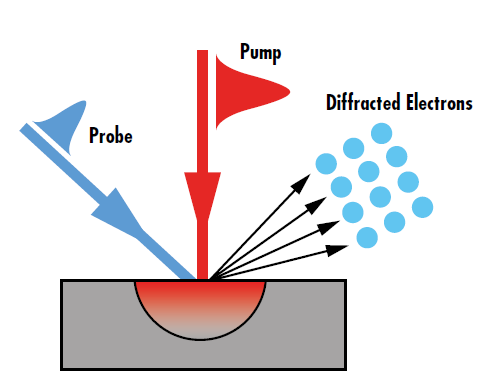
Figure 4 : Le changement d’intensité de la diffraction observé dans la spectroscopie pompe-sonde est directement lié au transport d’énergie hors équilibre causé par l’excitation laser ultrarapide

Le changement d’intensité de la diffraction causé par le laser ultrarapide est régi par l’effet Debye-Waller et s’exprime ainsi :

• I(t) est l’intensité de la diffraction au temps t
• I₀ est l’intensité initiale
• T₀ est la température initiale
• u² (T) est le déplacement quadratique moyen atomique exprimé comme suit :

• ħ est la constante de Planck réduite ou constante de Planck divisée par 2π
• m est la masse effective de la cellule unitaire
• k_B est la constante de Boltzmann
• θ_D est la température de Debye

Les Équation 4 et Équation 5 indiquent le changement de l’intensité diffractée suite à l’excitation laser à des délais pompe-sonde différents. Le changement d’intensité de la diffraction sera également différent selon que les faisceaux de la sonde et de la pompe éclairent la surface traitée de l’optique ou l’interface traitement/substrat (Figure 5). Le délai du système pour atteindre la température d’équilibre après une excitation ultrarapide est beaucoup plus long que la durée de l’impulsion ultrarapide. Le chauffage du nanofilm a lieu à une échelle de temps de l’ordre de la picoseconde et résulte de l’équilibrage de l’électron excité suite à une excitation laser ultrarapide.

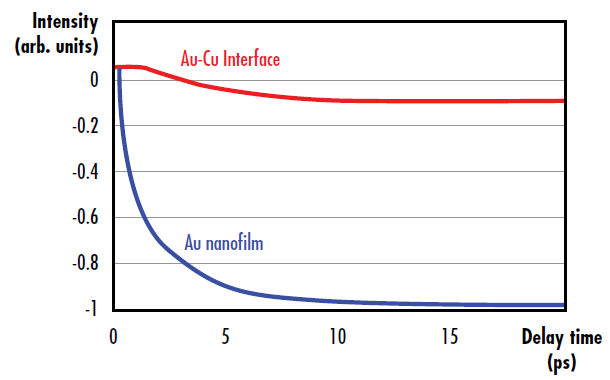
Figure 5 : Modification de l’intensité de la diffraction due à la diffusion électron-phonon et phonon-phonon suite à l’excitation ultrarapide dans un nanofilm d’or (bleu), ainsi que modification de l’intensité de la diffraction au niveau de l’interface or-cuivre due au transfert d’énergie du nanofilm d’or au substrat de cuivre (rouge)

Miroirs hautement dispersifs d’Edmund Optics^_®

VOIR MAINTENANT

Enregistrement d’un webinaire : Optiques ultrarapides : défis et solutions

REGARDER MAINTENANT

Références

1. Mao, S. S. et al., “Dynamics of Femtosecond Laser Interactions with Dielectrics.” Appl. Phys. A 2004, 79, 1695.
2. Jiang, L., and H. l. Tsai. “Energy Transport and Material Removal in Wide Bandgap Materials by a Femtosecond Laser Pulse.” International Journal of Heat and Mass Transfer, vol. 48, no. 3-4, 2005, pp. 487–499., doi:10.1016/j.ijheatmasstransfer.2004.09.016.
3. Wellershoff, Sebastian S., et al. “The Role of Electron–Phonon Coupling in Femtosecond Laser Damage of Metals.” Appl. Phys. A, vol. 69, Dec. 1999, pp. 99–107.
4. Shin, Taeho, et al. “Extended Two-Temperature Model for Ultrafast Thermal Response of Band Gap Materials upon Impulsive Optical Excitation.” The Journal of Chemical Physics, vol. 143, no. 19, 2015.
5. Karam, Tony E, et al. “Enhanced Photothermal Effects and Excited-State Dynamics of Plasmonic Size-Controlled Gold–Silver–Gold Core–Shell–Shell Nanoparticles.” J. Phys. Chem, vol. 119, 17 July 2015, pp. 18573–18580., doi: 10.1021/acs.jpcc.5b05110.
6. Heilpern, Tal, et al. “Determination of Hot Carrier Energy Distributions from Inversion of Ultrafast Pump-Probe Reflectivity Measurements.” Nature Communications, vol. 9, no. 1, Oct. 2018, doi:10.1038/s41467-018-04289-3.
7. Hu, Jianbo, et al. “Ultrafast Lattice Dynamics of Single Crystal and Polycrystalline Gold Nanofilms☆.” Chemical Physics Letters, vol. 683, 2017, pp. 258–261., doi:10.1016/j.cplett.2017.04.021.
8. Gedik, Nuh. “Techniques.” Gedik Group, Massachusetts Institute of Technology, 2013, web.mit.edu/gediklab/research.html

Section précédente Section suivante