Les propriétés thermiques des substrats optiques
Cette note d’application correspond aux sections 8.2, 8.3 et 8.4 du Guide des Ressources en Optique Laser.
Les coefficients de dilatation thermique
Pour les applications sujettes aux fluctuations de température, il convient de développer un système optique athermique. Les systèmes optiques athermiques sont insensibles aux changements thermiques d’un environnement et à la défocalisation qui en résulte. Le développement d’une conception athermique, qui dépend du coefficient de dilatation thermique (ou CTE pour Coefficient of Thermal Expansion) et du changement d’indice en fonction de la température $ \left( \tfrac{\text{d} n}{ \text{d} T} \right) $ des matériaux, est particulièrement critique dans l’infrarouge.
Le CTE est un terme général désignant l'une des trois mesures de la variation fractionnelle de la taille, de la surface ou du volume d'un matériau en raison d'un changement de température. Cependant, les fournisseurs de verre optique et les concepteurs d'optiques ne spécifient et n'utilisent que le coefficient de dilatation thermique linéaire (CLTE, abrégé dans l'industrie des polymères), qui est défini comme suit :
$ \small{\alpha_{L}}$ est le CET linéaire, $ \small{L} $ est la longueur dans une dimension, $ \small{T} $ est la température, et $ \tfrac{\text{d} L}{\text{d} T} $ est la réciproque du gradient de température par rapport à la dimension $ \small{L} $.
$ \small{\alpha_{A}}$ est le CTE de la surface, $ \small{A} $ est la surface en deux dimensions, et $ \tfrac{\text{d} A}{\text{d} T} $ est l'inverse du gradient de température par rapport à la surface.
$ \small{\alpha_{V}}$ est le CTE volumétrique, $ \small{V} $ est le volume en trois dimensions, et $ \tfrac{\text{d} V}{\text{d} T} $ est l'inverse du gradient de température par rapport au volume. Pour les matériaux isotropes, y compris la plupart des verres et des métaux, la relation entre le CTE est indiquée dans l'Équation 4.
En pratique, notamment pour les petites variations de température, les termes différentiels pour le changement de longueur et le changement de température ($\small{\text{d}L}$ et $\small{\text{d}T}$ respectivement) sont généralement bien approchés par les différences ($\small{ \Delta L}$ et $\small{ \Delta T}$ respectivement) observées dans l'Équation 5.
(5)$$ \alpha_L \approx \frac{1}{L} \frac{\Delta L}{\Delta T} $$
En général, lorsqu’un objet s’échauffe, il devient plus grand en raison de l’augmentation de l’énergie cinétique que subissent les molécules qui le constituent (Figure 1). Cependant, il existe quelques rares exceptions où il existe une relation inverse entre la température et la longueur, comme dans le cas de l'eau, dont le CDT linéaire devient négatif en dessous de 3,983°C et provoque une dilatation lorsque la température descend en dessous de 3,983°C.
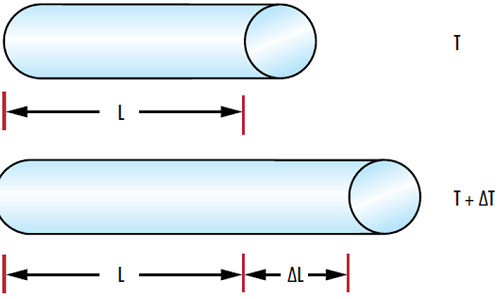
Figure 1 : Les changements de température $ \left( \small{ \Delta T \small} \right) $ conduisent à un changement de longueur d'un matériau $ \left( \small{ \Delta L} \right) $ basé sur le CTE linéaire du matériau.
Le CTE linéaire est exprimé en unités de $ \tfrac{1}{ ˚ \text{C}}$ ou $ \tfrac{1}{ \text{K}}$. Lors de la sélection d’une optique pour votre application, il est important de prendre en compte le CTE, car une modification de la taille de l’optique peut influencer l’alignement et les contraintes exercées sur le composant. Dans les environnements impliquant des variations de température, les utilisateurs doivent être sûrs que leur optique ne se dilatera pas lorsqu’elle sera chauffée. Une optique de 25 mm à température ambiante pourra être de 25,1 mm à 300 °C, ce qui pourrait briser la monture ou biaiser la lumière dans une direction non souhaitée, affectant ainsi la stabilité du pointage ou l’alignement du laser. C’est la raison pour laquelle un CTE faible est généralement préférable.
Coefficient thermique d’un indice de réfraction
Le coefficient thermique de l'indice de réfraction $ \left( \tfrac{\text{d} n}{\text{d} T} \right) $ est une mesure de la variation de l'indice de réfraction en fonction de la température. Le $ \tfrac{\text{d} n}{\text{d}T} $ de la plupart des matériaux IR est d’un ordre de grandeur supérieur à celui des verres visibles, ce qui crée de grandes variations de l’indice de réfraction. L'augmentation ou la diminution de l'indice de réfraction des verres avec l'augmentation de la température dépend du matériau spécifique, mais la plupart des types de verre auront des indices de réfraction plus élevés à des températures plus élevées.1 Lors de la conception d’objectifs athermalisés, les verres avec des coefficients de température positifs et négatifs sont appariés ensemble pour équilibrer le changement d'indice de réfraction de chacun d'entre eux.
L'équation complète de $ \tfrac{\text{d} n}{\text{d}T} $ d'un matériau est donnée par :
Où
$ \small{ T_0 }$ est la température de référence (20℃)
$\small{T}$ est la température en ℃
$\small{\Delta T}$ est la différence de température $ \left( \small{T} - \small{T_0} \right)$
$\small{\lambda}$ est la longueur d'onde de la lumière dans le vide
$ \small{D_0, D_1, D_2, E_0, E_1,} $ et $ \small{\lambda} _{\small{\text{TK}}} $ sont des constantes matérielles ajustées empiriquement
Le $ \tfrac{\text{d} n}{\text{d} T} $ n’est pas pertinent pour les optiques réfléchissantes, sauf en cas de variations de performances mineures dues à un changement de l’indice de réfraction du traitement. Cependant, il s’agit d’une propriété importante pour les optiques à transmission, car il permet de déterminer leur stabilité lorsqu’elles sont soumises à des variations de température. Il y aura toujours une certaine absorption avec un faisceau laser de forte puissance incident sur une optique, entraînant une augmentation de la température ; le $ \tfrac{\text{d} n}{\text{d} T} $ détermine dans quelle mesure cela affecte les performances (Figure 2).
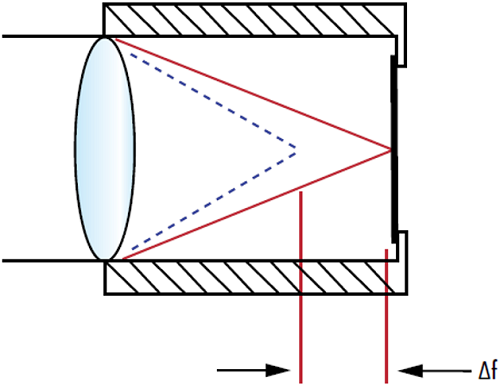
Figure 2 : La modification de l’indice de réfraction d’un composant optique en fonction de la température $ \left( \tfrac{\text{d} n}{\text{d} T} \right) $ peut entraîner un déplacement de la distance focale de l’objectif (∆f), ce qui modifie la position de la focalisation
Conductivité thermique
La conductivité thermique $ \left( \small{k} \right) $ d’un matériau est une mesure de sa capacité à transférer la chaleur par conduction (Figure 3). Elle est généralement mesurée en $ \tfrac{\text{W}}{ \left( \text{m} \, \cdot \, \text{K} \right)} $ or $ \tfrac{\text{Btu}}{\left( \text{hr} \, \cdot \, \text{ft} \, \cdot \, \text{˚F} \right)} $ et est utilisée pour définir le taux de conduction thermique :
$ \small{Q} $ représente la quantité de chaleur transférée dans le temps $ \small{t} $, et les unités de $ \tfrac{Q}{t} $ sont $ \tfrac{\text{J}}{\text{s}} $, ou $ \small{\text{W}} $. $ \small{A} $ est la section transversale du substrat, $ \small{\Delta T} $ est la différence de température entre une face du matériau et l'autre, et $ \small{d} $ est l'épaisseur du matériau.
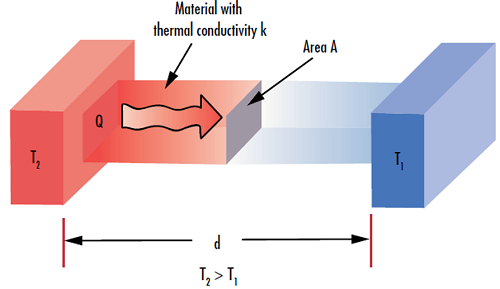
Figure 3 : La conductivité thermique d'un matériau $ \left( \small{k} \right) $ définit sa capacité à transférer la chaleur $ \left( \small{Q} \right) $ à travers une épaisseur donnée $ \left( \small{d} \right) $
Les matériaux à forte conductivité thermique, comme les métaux, sont capables de dissiper la chaleur beaucoup plus rapidement que les matériaux à faible conductivité thermique, comme les verres ou les plastiques. Comme l’un des principaux effets de la transmission du rayonnement laser à travers une optique est la conversion de l’énergie radiative en énergie thermique, il est important de connaître la conductivité thermique d’un matériau afin d’évaluer le bilan énergétique autour de l’optique dans les applications d’optique laser. Les matériaux qui ne réfléchissent ou ne transmettent pas de longueurs d’onde spécifiques absorbent plus de lumière et se réchauffent plus rapidement ; les verres colorés et les filtres absorbants en sont des exemples. Si une accumulation de chaleur à l’état non stationnaire se produit dans l’optique, des dommages seront rapidement causés, surtout sans l’ajout d’un système de refroidissement efficace. Même dans ce cas, si les composants optiques sont non homogènes, leur capacité à conduire la chaleur n’est pas uniforme et les points chauds du matériau pourraient rapidement et de manière plus importante endommager le composant. Comme pour le coefficient thermique de l’indice de réfraction, il est important de comprendre la conductivité thermique pour modéliser les systèmes laser de haute puissance et comprendre les effets de performance optique à attendre.
Références
- “TIE-19: Temperature Coefficient of the Refractive Index.” Schott, July 2016.
Plus de ressources
- Absorption (optique)
- Verre optique
- Le bon matériau pour les applications infrarouges (IR)
- Une introduction à l’athermalisation passive
- Homogénéité et dispersion due aux inclusions et aux bulles
- Dommages sous la surface
- Dispersion
- Matériaux d'optique laser courants
- Silice Fondue indice UV ou IR
- Série Vidéo de Labo Optique Laser













 Section précédente
Section précédente

ou consulter les numéros d’autres pays
facile à utiliser
entrer les numéros de stock pour commencer
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
L'entreprise Edmund Optics GmbH en Allemagne agit comme un mandataire d'Edmund Optics Ltd au Royaume-Uni. Le titulaire du contrat est Edmund Optics Ltd au Royaume-Uni.