Custom Bandpass Filter using Shortpass and Longpass Filters
Bandpass filters are optical filters that allow transmission of a specific range of wavelengths, or band, while blocking other wavelengths. Many off-the-shelf bandpass filter options are available, but when an application has specific requirements for bandwidth or center wavelength not readily available, Longpass and Shortpass filters can be stacked creating a customized bandpass filter. Longpass filters are optical filters that reflect short wavelengths while transmitting, or passing, long wavelengths. Conversely, Shortpass filters transmit short wavelengths but reflect long ones. Examples of both are represented in Figure 1.


Figure 1: Transmission Comparison of Shortpass and Longpass Filters
The transmission graphs are very similar to Heaviside functions (denoted as H(λ)) in mathematics. As shown in Equation 1, Heaviside functions are specialized piecewise functions that have a value of one for a certain domain and zero for the rest. The domain is determined by the constant x.
H(λ) can be denoted as the transmission of a filter and λ as the wavelength. Figure 2 shows a Heaviside model of the LWP graph from Figure 1.
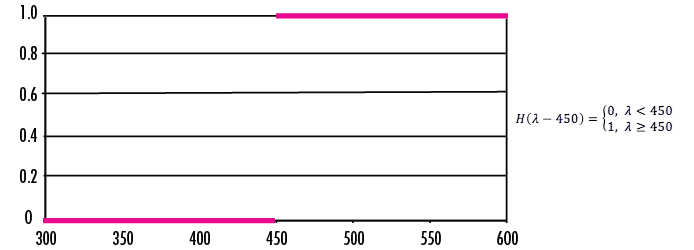
Figure 2: Heaviside model of the Longpass curve from Figure 1
A custom optical bandpass filter can be made by using at least two filters. This is conceptually very similar to multiplying Heaviside functions in mathematics. In order to obtain a rectangular function from 540 to 545, the two Heaviside functions must be multiplied together as shown in Equation 2 and Figure 3.

Figure 3: This graph is of the rectangular function of BP1,2
What is achieved through multiplication in mathematics is achieved physically by layering two or more optical filters. When layering multiple optical filters, light propagates through one filter and into the next. Because each filter transmits certain wavelengths, layering allows for the transmission of a customized band of wavelengths.

Figure 4: A custom bandpass filter where f1 and f2 represent Longpass and Shortpass filters
This results in a transmission curve represented in Figure 5.

Figure 5: The transmission curves of a custom bandpass filter produced by stacking a 450nm Longpass and 500nm Shortpass Filter
Stacking Longpass and Shortpass filters can quickly create a custom solution for selecting a specific bandpass and is an ideal alternative in scenarios where an off-the-shelf bandpass filter doesn't meet the application's requirements or a customer filter design is too expensive or has too long of a lead time.





















































































































ou consulter les numéros d’autres pays
facile à utiliser
entrer les numéros de stock pour commencer
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
L'entreprise Edmund Optics GmbH en Allemagne agit comme un mandataire d'Edmund Optics Ltd au Royaume-Uni. Le titulaire du contrat est Edmund Optics Ltd au Royaume-Uni.