Courbes FTM et performances des objectifs
Cette note correspond à la Section 2.6 du Guide de Ressources en Imagerie.
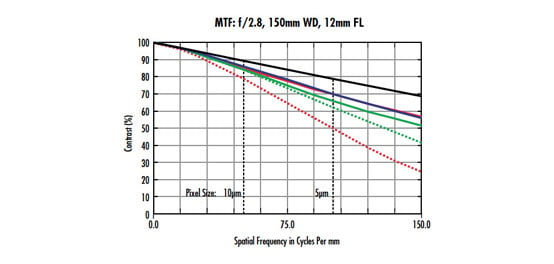
La Figure 1 est un exemple de courbe de fonction de transfert de modulation (FTM) pour un objectif de 12 mm utilisé sur le capteur Sony IMX250 (format 2/3" et pixels de 3,45 µm). Le format des capteurs est décrit dans Capteurs. La courbe montre le contraste de l'objectif sur une plage de fréquences de 0 à 150$ \small{\tfrac{\text{lp}}{\text{mm}}} $ (la résolution limite/Nyquist du capteur est de 145$ \small{\tfrac{\text{lp}}{\text{mm}}} ) $. En outre, le f/# de cet objectif est fixé à 2,8 et le grossissement à 0,05X. Le champ de vision (FOV), d'environ 170 mm, est environ 20 fois supérieur aux dimensions horizontales du capteur. Ce $ \small{\tfrac{\text{FOV}}{\text{grossissement}}} $ sera utilisé pour tous les exemples de cette section. Une lumière blanche est utilisée pour la source de lumière simulée.
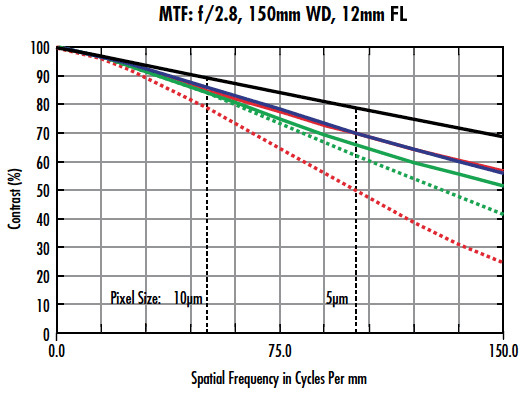
Figure 1 : Courbe MTF pour un objectif de 12 mm utilisé dans le capteur Sony IMX250.
Cette courbe fournit une variété d'informations. La première chose à noter est que la ligne noire limitée par la diffraction indique que le contraste théorique maximal réalisable est de presque 70% à la fréquence 150 et qu'aucune modification de la conception de cet objectif ne peut améliorer ses performances (en supposant un f/# et une longueur d'onde constants). Les lignes bleues, vertes et rouges sont également importantes et correspondent à la façon dont cet objectif se comporte sur le capteur (voir La fonction de transfert de modulation pour connaître les positions de champ correspondant à chaque couleur). Il est clairement démontré qu'à des fréquences plus basses et plus élevées, la reproduction du contraste n'est pas la même sur l'ensemble du capteur, donc pas la même sur le FOV.
Comparaison des conceptions et des configurations d'objectifs
Ex. 1 : Comparaison de deux objectifs ayant la même distance focale et le même f/#
La Figure 2 examine deux objectifs différents de la même distance focale, 12 mm, et f/#, f/2.8, sur le même capteur, et avec le même FOV. Ces objectifs produisent des systèmes de même taille mais dont les performances diffèrent. En analyse, la ligne horizontale bleu clair à 30% de contraste dans la Figure 2a montre qu'un contraste d'au moins 30% est réalisable sur la quasi-totalité du FOV, ce qui signifie que le capteur est pleinement exploité. Pour la Figure 2b, le champ complet est presque en dessous de 30% de contraste. Une meilleure qualité d'image ne pourra être obtenue que sur une petite partie du capteur. Notez que la boîte orange sur les deux courbes représente la fréquence d'interception (à un contraste de 70%) de l’objectif moins performant de la Figure 2b. Lorsque cette même boîte est placée dans la Figure 2a, on peut constater une énorme différence de performance entre les deux objectifs, même à des fréquences plus basses. La raison de la différence entre ces objectifs est le coût associé aux deux conceptions et aux variations de fabrication ; la Figure 2a est associée à une conception plus complexe et à des tolérances de fabrication plus serrées. L'objectif de la Figure 2a excelle à la fois dans les applications de basse et de haute résolution où des distances de travail (WD) relativement courtes pour des FOV plus larges sont nécessaires. La Figure 2b fonctionnera mieux lorsqu'un plus grand nombre de pixels est nécessaire pour améliorer la fidélité des algorithmes de traitement d'images et lorsqu'un coût moindre est requis. Les deux objectifs sont des conceptions valables pour des situations où elles constituent le bon choix ; tout dépend de l'application. Le fait qu'un objectif n'atteigne pas la limite de Nyquist sur un capteur n'exclut pas son utilisation sur ce capteur.


Figure 2 : Courbes FTM pour deux objectifs différents (a et b) avec la même distance focale, le même f/#, sur le même capteur et en utilisant les mêmes paramètres de système.
Ex. 2 : Comparaison de deux conceptions d'objectifs haute résolution au même f/# mais à des distances focales différentes
La Figure 3 examine deux objectifs haute résolution différents avec des distances focales de 12 mm et 16 mm, et les mêmes FOV, capteurs et f/#. En observant le contraste de l'objectif à la limite de Nyquist dans la Figure 3b (la ligne bleu clair), on constate une nette augmentation des performances par rapport à la Figure 3a. Si la différence absolue n'est que de 25% de contraste, la différence relative est plus proche de 85% si l'on considère le passage d'un contraste d'environ 25% à 46%. Cette boîte orange est placée là où la Figure 3a atteint un contraste de 70%. Notez que la différence de performance dans cet exemple n'est pas aussi extrême que dans le précédent. Le compromis entre ces objectifs est que la WD pour l’objectif de la Figure 3b a une augmentation d'environ 33% mais avec une augmentation décente de la performance. Cela suit les directives générales décrites dans la note Les meilleures pratiques pour une meilleure imagerie.
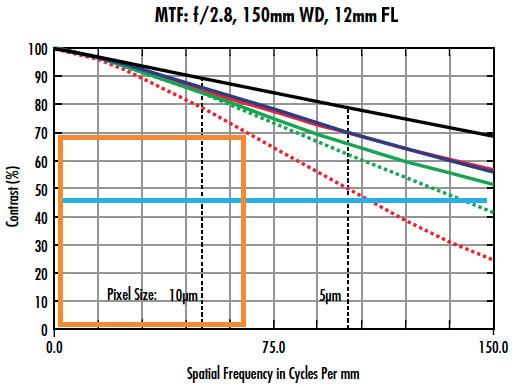
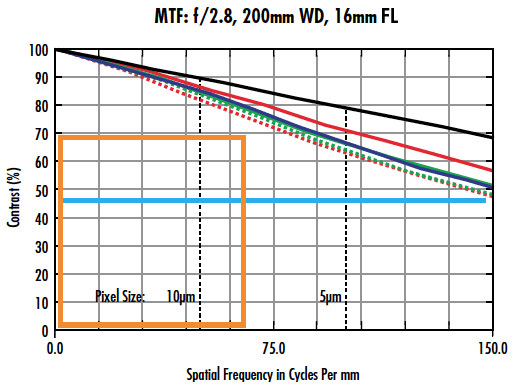
Figure 3 : Deux conceptions différentes d’objectifs à haute résolution avec différentes distances focales pour les mêmes f/# et paramètres de système.
Ex. 3 : Comparaison de différents f/# d'un même objectif de 35 mm
La Figure 4 présente la FTM d'un objectif 35 mm en lumière blanche à f/4 (a) et f/2 (b). La ligne jaune des deux graphiques montre le contraste limité par diffraction à la limite de Nyquist pour la Figure 4a , tandis que la ligne bleue indique la performance réelle la plus faible à la limite de Nyquist du même objectif à un f/4 dans la Figure 4a. Alors que la limite théorique de la Figure 4b est bien plus élevée, la performance est bien moindre. Cet exemple montre que des f/# plus élevés peuvent réduire les effets d'aberration, augmentant ainsi considérablement les performances de l'objectif, même si la limite de performance théorique est fortement réduite. La principale conséquence de la diaphragmatisation de l'objectif (augmentation du f/#), outre la résolution, est la diminution du débit de lumière.
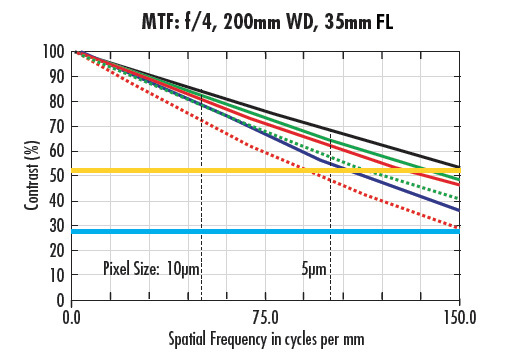
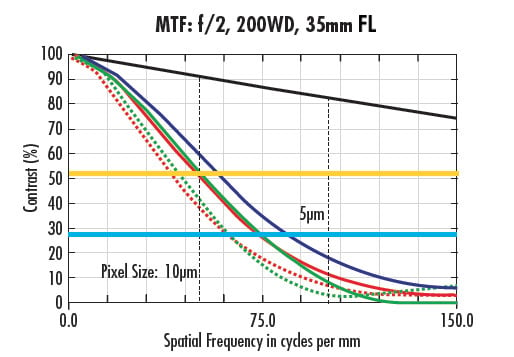
Figure 4 : Courbes FTM pour un objectif de 35 mm à la même WD et à différents f/# : f/4 (a) et f/2 (b).
Ex. 4 : L'effet de la modification de la distance de travail sur la FTM
Pour la Figure 5, les WD de 200 mm (a) et 450 mm (b) sont examinés pour le même modèle d'objectif de 35 mm à f/2. La grande différence de performance est directement liée à la capacité d'équilibrer le contenu d’aberration dans une conception d’objectif sur une gamme de WDs. Le changement de la WD, même avec une remise au point, entraînera des variations ou des réductions des performances, car l'objectif s'éloigne de la plage prévue. Ces effets sont plus profonds à des f/# inférieurs.
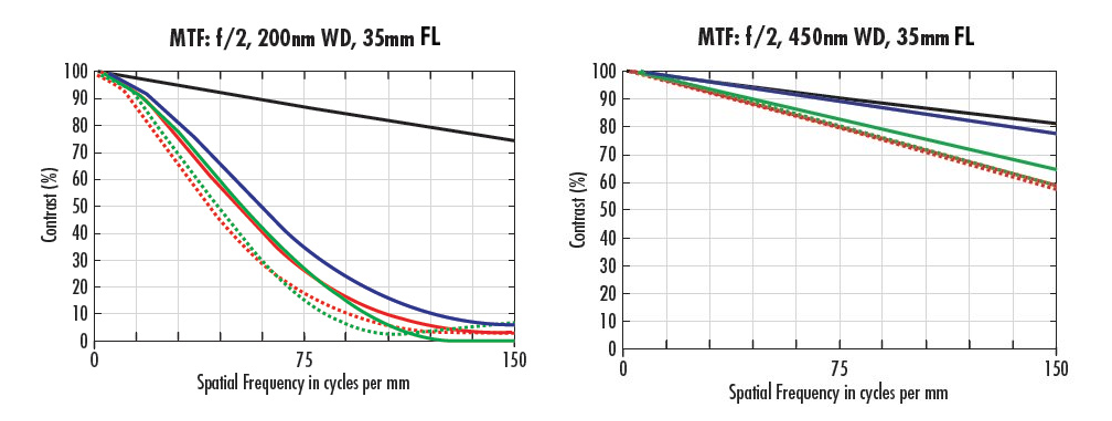
Figure 5 : Courbes FTM pour un objectif de 35 mm de distance focale à f/2 avec différentes WD.
Effets de la longueur d'onde sur les performances
Les différentes longueurs d'onde se courbent à des angles différents lorsque la lumière traverse un milieu (verre, eau, air, etc.). C'est ce que l'on observe lorsque la lumière du soleil traverse un prisme et crée un effet d'arc-en-ciel ; les longueurs d'onde les plus courtes sont davantage courbées que les plus longues. Ce même effet complique la résolution et la collecte d'informations dans les systèmes d'imagerie. Pour éviter ce problème, les systèmes d'imagerie et de vision industrielle utilisent un éclairage monochromatique (à une seule longueur d'onde) ou à bande étroite. L'éclairage monochromatique (par exemple, à partir d'une LED de 660 nm) élimine pratiquement les aberrations chromatiques d'un système d'imagerie.
Aberration chromatique
Les aberrations chromatiques existent sous deux formes : le décalage latéral des couleurs (Figure 6) et le décalage chromatique focal (Figure 7).
Le décalage latéral des couleurs, Figure 6, est observé en se déplaçant du centre d'une image vers le bord de celle-ci. Au centre, les points correspondant aux différentes longueurs d'onde de la lumière sont concentriques. En se déplaçant vers le coin de l'image, les longueurs d'onde se séparent et produisent un effet d'arc-en-ciel. En raison de la séparation des couleurs, un point donné de l'objet est imagé sur une plus grande surface, ce qui réduit le contraste. Sur les capteurs dont les pixels sont plus petits, ce résultat est encore plus prononcé, car le flou se propage sur un plus grand nombre de pixels. Vous trouverez des détails sur la couleur latérale dans la section Aberrations.

Figure 6 : Représentation d'un point subissant un changement de couleur latéral à différents points du champ.
Le décalage focal chromatique, Figure 7, concerne la capacité d'un objectif à focaliser toutes les longueurs d'onde à la même distance de l’objet. Des longueurs d'onde différentes auront des plans de focalisation différents. Ce décalage de la mise au point par rapport à la longueur d'onde entraîne une réduction du contraste, car les différentes longueurs d'onde créent des points de tailles différentes dans le plan de l'image où se trouve le capteur de la caméra. Dans le plan de l'image de la Figure 7, on voit une petite taille de point dans les longueurs d'onde rouges, une plus grande taille de point en vert, et la plus grande taille de point en bleu. Les couleurs ne seront pas toutes focalisées en même temps. Plus de détails peuvent être trouvés dans Aberrations.

Figure 7 : Représentation d'un point subissant un décalage focal chromatique à différentes profondeurs.
Choisir la longueur d'onde optimale
L'éclairage monochromatique améliore le contraste en éliminant à la fois le décalage focal chromatique et l'aberration chromatique latérale. Envisagez d'utiliser un éclairage LED, des lasers ou des filtres. Cependant, différentes longueurs d'onde peuvent avoir des effets FTM différents dans un système. La limite de diffraction définit le plus petit point théorique qui peut être créé par un objectif parfait, défini par le diamètre de la tache d'Airy, qui dépend de la longueur d'onde (λ). En utilisant l'équation 1, on peut analyser la variation de la taille du point pour différentes longueurs d'onde et différents f/#.
Le Tableau 1 présente le diamètre calculé de la tache d'Airy pour des longueurs d'onde allant du violet (405 nm) au proche infrarouge (880 nm) à différents f/#s. Ces données montrent que les systèmes d’objectifs ont une meilleure résolution théorique et de meilleures performances lorsqu'ils sont utilisés avec des longueurs d'onde plus courtes. Les longueurs d'onde plus courtes permettent une meilleure utilisation des pixels du capteur, quelle que soit leur taille, en raison de la taille réduite du point réalisable. Ce phénomène est particulièrement prononcé sur les capteurs ayant de très petits pixels. L'utilisation des f/# plus élevés permet d'obtenir un DOF plus important. Une LED rouge peut être utilisée à un f/2,8 pour générer un point de 4,51 µm ou une LED bleue peut générer presque la même taille de point à un f/4. Si les deux options donnent des niveaux de performance acceptables à la meilleure mise au point, le système réglé à f/4 en utilisant la lumière bleue produira un meilleur DOF, ce qui pourrait être une exigence essentielle.
| Couleur | Longueur d’onde | Ouverture (f/#) | ||||
|---|---|---|---|---|---|---|
| f/1,4 | f/2,8 | f/4 | f/8 | f/16 | ||
| NIR | 880 | 3,01 | 6,01 | 8,59 | 17,18 | 34,36 |
| Rouge | 660 | 2,25 | 4,51 | 6,44 | 12,88 | 25,77 |
| Vert | 520 | 1,78 | 3,55 | 5,08 | 10,15 | 20,30 |
| Bleu | 470 | 1,61 | 3,21 | 4,59 | 9,17 | 18,35 |
| Violet | 405 | 1,38 | 2,77 | 3,95 | 7,91 | 15,81 |
Tableau 1 : Tailles théoriques des points définies par le diamètre de la tache d'Airy pour différentes longueurs d'onde et f/#s.
Ex. 5 : Amélioration avec la longueur d'onde
Les deux images de la Figure 8 sont prises avec les mêmes objectifs et la même caméra produisant le même FOV, présentant ainsi la même résolution spatiale sur l'objet. La caméra utilise des pixels de 3,45 µm. L'éclairage de la Figure 8a est réglé à 660 nm et celui de 8b à 470 nm. L'objectif haute résolution a été réglé sur un f/# plus élevé afin de réduire considérablement les effets d'aberration. Cela permet à la diffraction d'être la principale limitation du système. Les cercles bleus montrent la résolution limite de la Figure 8a. Notez que la Figure 8b présente une augmentation significative des détails résolubles (détail d’environ 50% plus fin). Même aux fréquences plus basses (lignes plus larges), on observe un niveau de contraste plus élevé avec l'éclairage à 470 nm dans la Figure 8b.


Figure 8 : Images de la mire étoilée prises avec le même objectif, au même f/#, avec le même capteur. La longueur d'onde varie de 660 nm (a) à 470 nm(b).
Ex. 6 : FTM lumière blanche et monochromatique
Dans la Figure 9, le même objectif est utilisé avec les mêmes WD et f/#. La Figure 9a montre une lumière blanche, et la Figure 9b montre un éclairage de 470 nm. Sur la Figure 9a, les performances sont à 50% de la limite de Nyquist (pour un pixel de 3,45 μm) ou en dessous. Pour la Figure 9b, la performance à la limite de Nyquist est supérieure à celle de la Figure 9a. De plus, la performance au centre du système de la Figure 9b est supérieure à la limite de diffraction de la Figure 9a. La raison de cette augmentation des performances est double : l'utilisation d'une lumière monochromatique élimine les aberrations chromatiques, ce qui permet de créer des points plus petits, et l'éclairage à 470 nm est l'une des plus courtes longueurs d'onde de la lumière utilisée dans le domaine visible pour l'imagerie. Comme détaillé dans les sections sur la limite de diffraction et la tache d'Airy, les longueurs d'onde plus courtes permettent une résolution plus élevée.
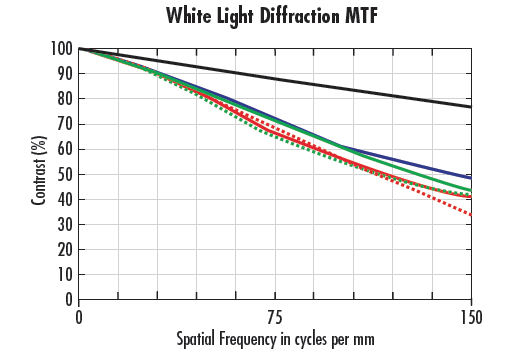
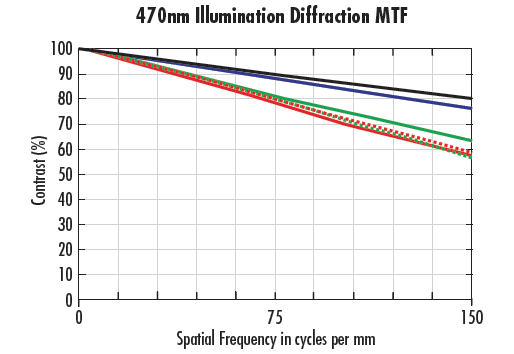
Figure 9 : Courbes FTM pour le même objectif à f/2 en utilisant différentes longueurs d'onde ; lumière blanche (a)et 470 nm (b).
Considérations relatives à la longueur d'onde
Le changement de longueur d'onde peut poser quelques problèmes. La conception des objectifs est d'autant plus difficile que la longueur d'onde de l'éclairage tend vers l'UV (lorsque la longueur d'onde diminue), même si la bande d'ondes est étroite : les matériaux en verre ont tendance à ne pas être aussi performants à des longueurs d'onde plus courtes (inférieures à environ 425 nm). Il existe des modèles dans cette région du spectre, mais leurs capacités sont souvent limitées et les matériaux rares utilisés rendent la fabrication des objectifs plus coûteuse. La meilleure performance théorique observée dans le Tableau 1 se situe à la longueur d'onde violette de 405 nm, mais la plupart des systèmes conçus ne sont pas performants dans cette zone. Il est très important d'évaluer ce qu'un objectif peut faire de manière réaliste à des longueurs d'onde aussi courtes en utilisant les courbes de performance des objectifs.
Ex. 7 : Limites théoriques
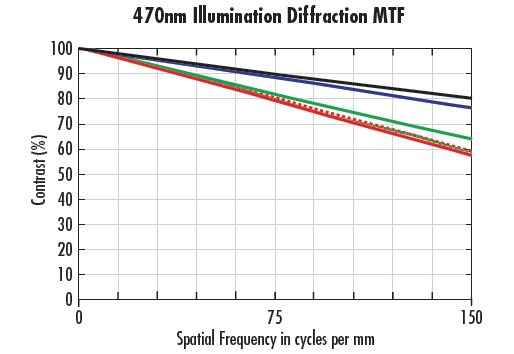
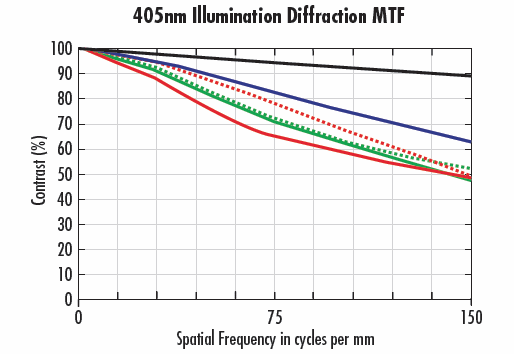
La Figure 10 compare un objectif 35 mm à f/2 avec des longueurs d'onde bleues (470 nm) et violettes (405 nm) (10a et 10b respectivement). Bien que la Figure 10a présente une limite de diffraction inférieure, elle montre également que la longueur d'onde de 470 nm donne de meilleures performances à toutes les positions de champ. L'effet est accru lorsque l'objectif est utilisé aux extrêmes de ses capacités de conception pour le f/# et la WD (détaillées dans La fonction de transfert de modulation). Un autre problème de longueur d'onde qui peut grandement affecter les performances est lié au décalage focal chromatique. Au fur et à mesure que la gamme de longueurs d'onde de l'application augmente, la capacité de l’objectif à maintenir des niveaux de performance élevés sera compromise. La note Aberrations sur les aberrations donne plus de détails sur le phénomène.













 Section précédente
Section précédente















ou consulter les numéros d’autres pays
facile à utiliser
entrer les numéros de stock pour commencer
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
POLITIQUE DE CONFIDENTIALITÉ | POLITIQUE DE COOKIES | CONDITIONS GÉNÈRALES | CONDITIONS GÉNÈRALES B2C | MENTIONS LÉGALES | ACCESSIBILITÉ
L'entreprise Edmund Optics GmbH en Allemagne agit comme un mandataire d'Edmund Optics Ltd au Royaume-Uni. Le titulaire du contrat est Edmund Optics Ltd au Royaume-Uni.