Tests et mires
Aperçu de mires de test
Cette note correspond à la Section 12.2 du Guide de Ressources en Imagerie.
Les mires de test permettent de déterminer les performances d'un système d'imagerie. Il peut s'agir de dépanner un système, d'étalonner, de certifier ou d'évaluer des mesures, ou d'établir une base pour garantir que plusieurs systèmes fonctionnent bien ensemble. La qualité de l'image pouvant être définie par différentes composantes, notamment la résolution, le contraste, la fonction de transfert de modulation (FTM), la profondeur de champ (DOF) ou la distorsion, des systèmes différents peuvent nécessiter des mires différentes. Certains systèmes peuvent en nécessiter plus d'une. Notez que les résultats de l'utilisation d'une mire de test sont subjectifs s'ils ne sont observés que visuellement ; l'observation visuelle dépend de la personne qui regarde la mire. Une personne ayant une bonne acuité visuelle est généralement capable de discerner une résolution plus élevée ou plus de détails qu'une personne ayant une faible acuité visuelle. De plus, les personnes qui regardent régulièrement ces mires peuvent avoir entraîné leur cerveau à interpoler des détails qui ne sont pas réellement présents, en raison de l'observation des motifs répétitifs de la mire. L'inspection visuelle peut aider à comparer deux systèmes différents mais ne permet pas toujours de valider les résultats. Il est important d'utiliser un logiciel pour valider réellement les mesures.
| Mires pour les mesures de résolution | |||
| Mire | Applications | Avantages | Inconvénients |
| USAF 1951 | Tests de résolution dans les systèmes de vision, les équipements de test optique, les microscopes, les objectifs vidéo à fort grossissement, la microscopie à fluorescence et confocale, la photolithographie et la nanotechnologie | Teste simultanément les résolutions verticale et horizontale à des fréquences spatiales discrètes | Il faut repositionner la mire pour évaluer pleinement les performances d'un système |
| Il peut être difficile de déterminer si l'ensemble du mire étoilée (FOV) est au point | |||
| Réseau de Ronchi | Test de la résolution et du contraste | Peut déterminer simultanément la meilleure mise au point du système sur l'ensemble du champ de vision | Une mire différente est nécessaire pour chaque fréquence à évaluer |
| Tests de diffraction | Les réductions de résolution non symétriques ne peuvent pas être analysées | ||
| Étoile | Comparaison de systèmes d'imagerie à haute résolution ou à fort grossissement | Potentiellement la plus puissante pour tester la résolution et le contraste | Il est difficile de déterminer la résolution exacte que le système d'essai atteint à chaque élément |
| Alignement du système | Peut évaluer un changement continu de résolution à travers plusieurs orientations sans repositionner la mire | ||
| Assistance au montage | Facilite la comparaison des différents systèmes d'imagerie | Nécessite un logiciel d'analyse d'image avancé | |
Tableau 1 : Les applications et les avantages et inconvénients des différentes mires de résolution.
La mire USAF 1951
Cette note correspond à la Section 12.3 du Guide de Ressources en Imagerie.
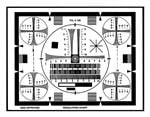
La mire USAF 1951 est l'une des mires de test les plus couramment utilisées. Elle est constituée d'ensembles de lignes horizontales et verticales, appelées éléments, de tailles variables (Figure 1).

Figure 1 : Exemple d'une mire USAF 1951.
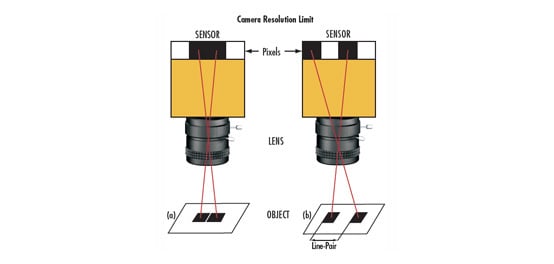
Les éléments horizontal et vertical sont utilisés par un système pour tester simultanément les résolutions verticale et horizontale à des fréquences spatiales discrètes (paires de lignes par millimètre, ou $ \small{ \tfrac{\text{lp}}{\text{mm}} } )$ dans le plan de l'objet. Chaque élément possède un ensemble unique de largeurs et d'espacements et est identifié par un numéro de 1 à 6. Six éléments numérotés séquentiellement sont considérés comme un groupe et chaque groupe a un numéro d'identification qui peut être positif, négatif ou nul. Ce numéro de groupe va de -2 à 7. Le numéro de groupe et le numéro d'élément sont ensuite utilisés ensemble pour déterminer la fréquence spatiale. La résolution est basée sur une paire de lignes (lp) qui équivaut à une barre noire et un espace blanc (Figure 2).
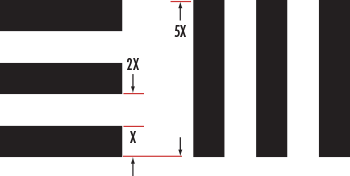
Figure 2 : Spécifications des mires USAF 1951.
Les barres verticales sont utilisées pour calculer la résolution horizontale, et les barres horizontales sont utilisées pour calculer la résolution verticale.
Qualitativement, la résolution d'un système d'imagerie est définie comme la combinaison de groupes et d'éléments qui se trouve juste avant que les barres noires et blanches ne commencent à s'estomper. Quantitativement, la résolution (en $ \small{ \tfrac{\text{lp}}{\text{mm}} } )$ peut être calculée par l'équation 1, où $\small{\xi} $, est la résolution en $ \small{ \tfrac{\text{lp}}{\text{mm}} }$, $\small{G}$ est le membre de groupe et $ \small{E} $ est le numéro de l‘élément.
Les mires USAF 1951 sont conçues de manière à ce que les éléments à haute résolution soient plus proches du centre de la mire, tandis que les éléments à faible résolution sont plus proches des bords de la mire. Cette disposition est avantageuse pour tester les objectifs de zoom, car elle évite de devoir repositionner la mire en permettant aux éléments de plus haute résolution de rester dans le champ de vision lorsque le grossissement de l'objectif réduit le champ de vision.
Exemple d'une mire USAF 1951
Les mires USAF 1951 présentent des inconvénients du fait que les éléments à haute résolution sont centrés. Les objectifs produisent différents niveaux de résolution au centre et aux coins du champ de vision. Le fait de s'éloigner du centre du champ entraîne généralement une diminution de la résolution, d'où l'importance de vérifier la résolution et le contraste dans de nombreuses positions du champ. Cela nécessite de repositionner la mire autour du champ de vision et de prendre plusieurs images pour évaluer les performances complètes d'un système, ce qui augmente la durée des tests. Cela peut également poser des problèmes selon que le système est mis au point au centre du champ de vision ou sur l'ensemble du champ ; comme la résolution varie sur le champ, il peut être difficile de déterminer quand le champ de vision complet est le mieux mis au point. Certains objectifs permettent d'obtenir une très haute résolution au centre du champ de vision, mais une très faible résolution dans les coins lorsque l'objectif et le système de caméra sont focalisés sur le centre de l'image. Défocalisez légèrement l'objectif pour équilibrer la résolution sur l'ensemble du champ. Cependant, cela se fait au détriment de la résolution centrale. La perte de la résolution centrale n'est cependant pas nécessairement mauvaise, car l'objectif peut encore répondre aux exigences de l'application tout en obtenant une mise au point équilibrée (Figure 3).

Figure 3a : Exemple d’une USAF 1951 : Le centre et le coin d'une image qui a été repositionnée de manière à ce que la meilleure mise au point se fasse uniquement au milieu de la mire.

Figure 3b : Le centre et le coin d'une image qui présente une mise au point équilibrée sur l'ensemble du champ.
Le potentiel de variabilité de la résolution dans le FOV renforce la nécessité d'analyser toutes les positions de champ avant de tirer des conclusions sur les performances d'un système. L'objectif qui fonctionne de manière optimale avec la mire au centre n'est pas forcément le plus performant dans l'ensemble. Cependant, il est essentiel d'effectuer toutes les analyses avec un seul réglage de la mise au point. Il peut sembler intuitif de déterminer les meilleures performances du système à travers le milieu de l'objectif, puis de refaire la mise au point pour voir les performances dans les coins, mais cela ne montrera pas comment le système se comportera une fois déployé, car il est souvent impossible de refaire la mise au point pendant le fonctionnement.
Il existe des variantes de cette mire qui permettent une analyse sur l'ensemble du FOV en répétant les motifs à de nombreux endroits de la mire (Figure 4).

Figure 4a : Une mire USAF 1951 disposée en roue.
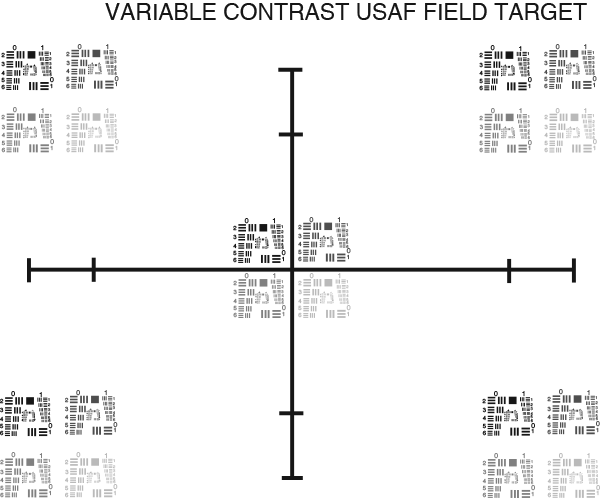
Figure 4b : Une mire USAF 1951 à contraste et champ variables.
Réseaux de Ronchi
Cette note correspond à la Section 12.4 du Guide de Ressources en Imagerie.
Certains problèmes associés à la mire USAF 1951 sont résolus en utilisant la mire connue sous le nom de Réseau de Ronchi. Cette mire comporte des lignes répétées à une fréquence spatiale dans une orientation qui couvre toute la surface de la mire (Figure 5). Comme il y a des détails sur l'ensemble de la mire, la meilleure mise au point du système sur l'ensemble du champ peut être évaluée. Pour les applications qui ne nécessitent qu'une seule fréquence analysée, il s'agit d'un outil simple et facile à utiliser. Toutefois, l'utilisation du Réseau de Ronchi présente deux inconvénients. Tout d'abord, comme une mire donnée ne fournit qu'une seule fréquence, une nouvelle mire est nécessaire pour chaque fréquence. Deuxièmement, les réductions de résolution non symétriques dans le champ qui sont le résultat de facteurs tels que l'astigmatisme ne peuvent pas être analysées car les lignes ne se propagent que dans une seule direction. Pour y remédier, la mire doit être tournée de 90° et une deuxième image doit être utilisée pour analyser la résolution. De plus, bien que la mise au point d'un objectif puisse être équilibrée pour une mise au point optimale, même pour les cas d'astigmatisme, il peut être difficile de trouver cet équilibre lors de l'alternance.

Figure 5 : Un réseau de Ronchi.
La mire étoilée.
Cette note correspond à la Section 12.5 du Guide de Ressources en Imagerie.
La mire étoilée de départ multi-éléments est probablement l'outil le plus puissant pour tester la résolution et le contraste d'un système et combine de nombreux atouts des mires USAF et de Ronchi. Chaque élément de la mire étoilée est constitué d'un cercle formé d'une alternance de coins positifs et négatifs en forme de tarte qui s'effilent vers le centre selon un angle connu (Figure 6). Les coins coniques de l'élément offrent un changement continu de résolution qui peut être évalué dans les directions verticale et horizontale, ainsi que dans une variété d'autres orientations, sans repositionner la mire.
La présence de nombreuses étoiles dans le champ de vision facilite la comparaison de différentes solutions d'imagerie en permettant de déterminer la meilleure mise au point dans le champ de vision tout en analysant simultanément les informations horizontales et verticales à diverses résolutions. La Figure 4 montre la mire étoilée complète ; les zones en surbrillance situées au centre, au milieu du bas et dans le coin de la mire sont comparées entre deux objectifs différents dans les images d'exemple supplémentaires. Pour ces exemples, un capteur monochrome Sony ICX625 avec des pixels de 3,45 µm et une résolution totale de 5MP ainsi qu'un rétroéclairage à lumière blanche sont utilisés.

Figure 6 : Une mire étoilée.
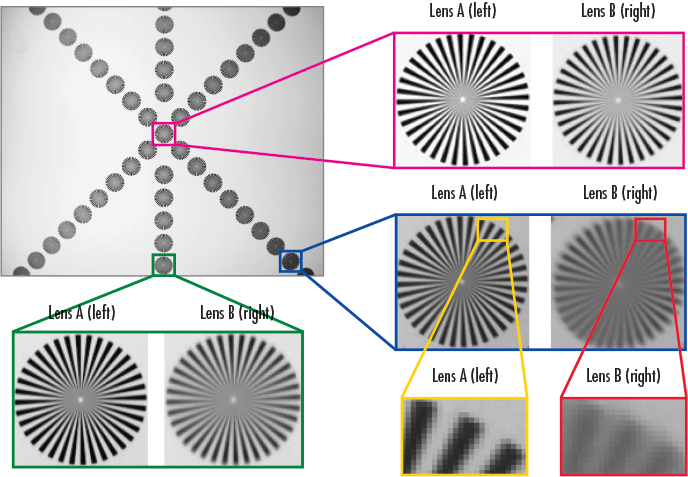
Figure 7 : Une mire étoilée est imagée avec deux objectifs (A et B) ayant la même distance focale, les mêmes f/#, FOV et capteurs. La supériorité de l'objectif A devient apparente le long du bord et dans le coin du capteur.
Limites de la mire étoilée
La mire étoilée a aussi ses inconvénients. Comme les coins fournissent des changements continus dans la résolution, il est plus difficile de déterminer la résolution exacte que le système de test atteint à chaque élément. Si cela peut être fait mathématiquement, ce n'est pas facile visuellement. En outre, la combinaison de la nature circulaire des éléments en étoile et du potentiel de flou non symétrique rend plus difficile l'utilisation d'outils logiciels simples, tels que les profileurs de lignes, pour extraire des informations de l'image. Un logiciel d'analyse d'image plus avancé est nécessaire pour exploiter pleinement la mire étoilée.
Mires de télécentricité
Cette note correspond à la Section 12.6 du Guide de Ressources en Imagerie.
Les mires de télécentricité permettent de visualiser et de mesurer avec précision les effets de keystone d'une image. L'importance des effets de keystone est liée à la télécentricité de l’objectif qui image la mire. La mire est placée à un angle de 45° par rapport à l'axe optique de sorte que le bas de la mire soit plus éloigné de l'objectif que le haut de la mire (Figure 8).

Figure 8 : Une mire de télécentricité placée sous un objectif.
Lors de l'imagerie de la mire à travers un objectif non télé-centrique, la distance entre les lignes verticales semble diminuer au bas de l'image (Figure 9) ; cet effet est connu sous le nom de keystone. Un objectif parfaitement télécentrique n'aura pas d’effet de keystone et la télécentricité sera de 0° (Figure 10).

Figure 9 : Cette image (prise avec un objectif de 8 mm de distance focale) illustre l’effet de keystone. Les lignes convergent clairement au bas de l'image. Le point central d’une ligne n'a pas la même position dans la partie inférieure de l'image que dans la partie supérieure.

Figure 10 : Il est évident que le flou dans cette image (prise avec un objectif télécentrique) est symétrique. Si vous prenez un profil de ligne horizontale à travers l'image et trouvez la composante horizontale du centre de chaque ligne noire, l'emplacement sera le même dans la partie floue de l'image et dans la partie focalisée de l'image.
Cette différence de position peut être convertie en un degré de télécentricité selon les étapes suivantes :
- Trouvez la distance entre votre profil de ligne supérieure et votre profil de ligne inférieure. $ \Delta Y = \left( Y_1 - Y_2 \right) $
- Trouvez le déplacement horizontal. $ \Delta X = \left| X_1 - X_2 \right| $
- Calculez l'angle télécentrique. $ \theta = \tan ^{-1} \left( \tfrac{\Delta X}{\Delta Y} \right) $
Mires de profondeur de champ
Cette note correspond à la Section 12.7 du Guide de Ressources en Imagerie.
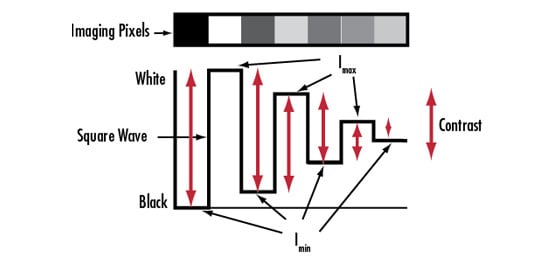
Les mires de profondeur de champ permettent de visualiser et de quantifier la manière dont la mise au point est maintenue lorsque les détails s'éloignent du plan sur lequel l'objectif est mis au point. Les mires de profondeur de champ consistent en des lignes de résolutions de fréquences connues qui sont inclinées selon un angle connu et sont utilisées pour déterminer le degré de maintien de la mise au point. Plus les lignes se rapprochent et s'éloignent de l'objectif, plus elles deviennent floues, jusqu'à ce qu'on ne puisse plus les distinguer les unes des autres. La mesure du contraste peut être effectuée à différentes distances pour déterminer à quel moment le niveau de résolution souhaité est perdu ; cela permet de déterminer la limite de la DOF pour un objectif à un réglage donné. Les Figures 11 et 12 montrent comment utiliser une mire de profondeur de champ.

Figure 11 : Une mire de profondeur de champ doit être à 45° de l'objectif.
Figure 12 : Exemples de configurations utilisant une mire de profondeur de champ.
Exemple : Utilisation d'une mire de profondeur de champ
Objectif 50 mm de la série DG
La Figure 13 montre une caméra montée verticalement et regardant vers le bas une mire de profondeur de champ qui a été placée à un angle de 45° par rapport à la trajectoire de l'image. L’objectif étant focalisé verticalement au milieu de la mire, l'image est floue en haut et en bas de la mire. Les images montrent trois réglages différents de f/# et la manière dont les ajustements de l'iris modifient la capacité à obtenir la DOF. Remarque : Les réseaux de Ronchi peuvent également être utilisées pour réaliser ce type d'essai, car elles ont des fréquences fixes et peuvent être inclinées pour créer cet effet ; plus l'inclinaison est grande, plus la partie de DOF pouvant être mesurée est important.
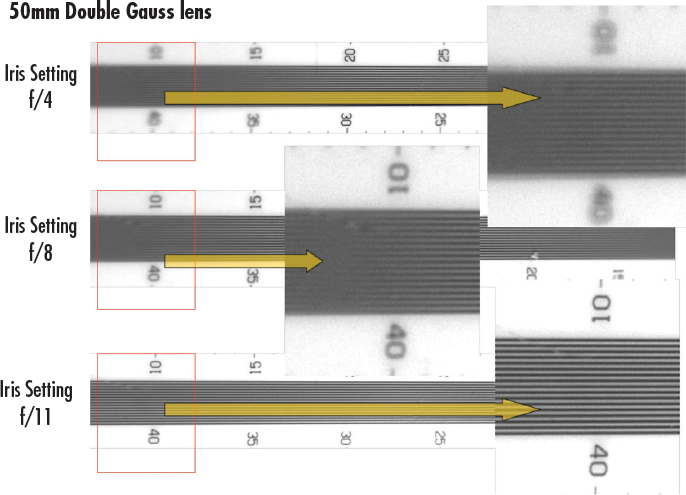
Figure 13 : Images d'une mire DOF prises avec un objectif de 50 mm à f/4, f/8 et f/11.
Allez sur www.edmundoptics.com/imaging-lab pour voir le module 1.8 du laboratoire d'imagerie d'EO sur la profondeur de champ.
Mires de distorsion
Cette note correspond à la Section 12.8 du Guide de Ressources en Imagerie.
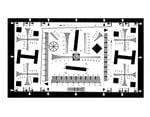
Les mires de distorsion sont utilisées pour calibrer les systèmes afin de mesurer correctement le mauvais positionnement optique des informations d'imagerie. Ces mires consistent en des motifs de points, de grilles ou de carrés ; elles sont compatibles avec les routines d'étalonnage de la plupart des logiciels d'imagerie ; et elles peuvent remapper ou ajuster les mesures dans le FOV (Figure 14).

Figure 14 : Une mire de distorsion à grille de points.
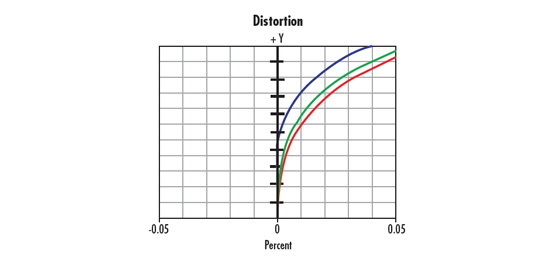
La Figure 15 montre les types de distorsion qui peuvent être réglés. Une fois le motif imagé, la taille et l'espacement connus du motif permettent d'effectuer des ajustements (Figure 15).
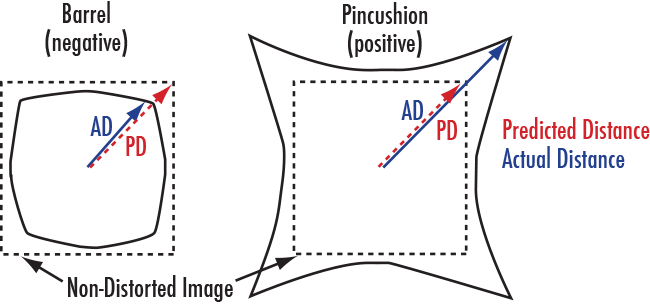
Figure 15 : Types de distorsion.













 Section précédente
Section précédente

















































ou consulter les numéros d’autres pays
facile à utiliser
entrer les numéros de stock pour commencer
Copyright 2023 | Edmund Optics SARL, 76-78 rue d’Alsace, 69100 Villeurbanne, France
L'entreprise Edmund Optics GmbH en Allemagne agit comme un mandataire d'Edmund Optics Ltd au Royaume-Uni. Le titulaire du contrat est Edmund Optics Ltd au Royaume-Uni.