Qualité de faisceau et rapport de Strehl

Afin de prédire précisément la performance et la qualité réelles d’un laser, il est nécessaire de comprendre le facteur M² de ce laser, qui décrit la qualité du faisceau. Une fois que les performances du laser sont connues, le fait de définir la performance réelle de n’importe quel système optique utilisé avec lui permettra de comprendre la performance du système final. La comparaison de la performance réelle d’un système optique à sa performance idéale limitée par la diffraction s’effectue grâce au rapport de Strehl. 

Facteur M²

La qualité d’un faisceau laser est caractérisée par le facteur M², qui compare la vraie forme du faisceau à celle d’un faisceau gaussien idéal. La norme ISO 11146 définit le facteur M² comme suit¹:

Dans l'Équation 1, w₀ est le waist du faisceau, θ est l’angle de divergence du laser et λ est la longueur d’onde de l’émission laser (Figure 1). Comme défini dans notre note d’application Propagation d’un faisceau gaussien, l’angle de divergence d’un faisceau gaussien est déterminé par l’équation suivante :

L’insertion de l’angle de divergence trouvé dans l'Équation simplifie l’équation du facteur M² d’un faisceau gaussien :

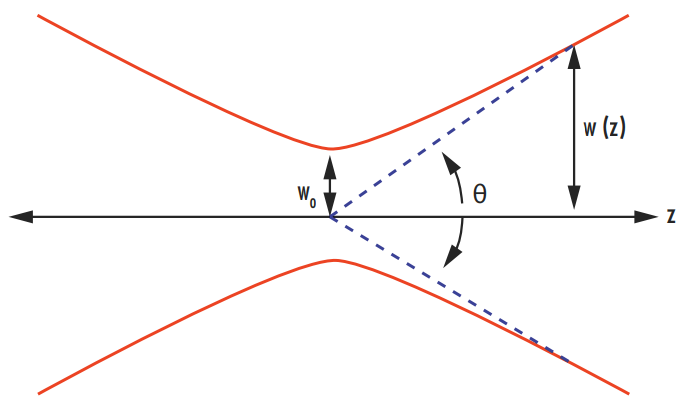
Figure 1 : Illustration de l’angle de divergence et du waist d’un faisceau laser

Ainsi, un facteur M² correspond à un faisceau gaussien limité par la diffraction. Des facteurs M² plus élevés (supérieurs à 1) correspondent aux déviations d’un faisceau gaussien. Il est impossible d’obtenir une valeur inférieure à 1. Le facteur M² d’un mode Hermite-Gaussien est donné par (2n + 1) dans la direction x et par (2m + 1) dans la direction y.² Par exemple, TEM₁₃ présente un facteur M² de 3 dans la direction x et de 7 dans la direction y. Un laser hélium-néon typique présente un facteur M² compris entre 1 et 1,1. Vous trouverez plus d’informations sur les modes Hermite-Gaussiens dans notre note d’application Modes de résonateurs laser.

En combinaison avec la puissance optique du faisceau laser, le facteur M² détermine la radiance du faisceau. Le facteur M² peut également être utilisé pour estimer le rayon d’un faisceau lorsqu’il se propage, en remplaçant la longueur d’onde d’un laser par la longueur d’onde multipliée par le facteur M², calculé dans toutes les équations de la note d’application Propagation d’un faisceau gaussien.³

Le facteur M² est important, car il représente la manière dont un faisceau laser peut être focalisé à une divergence donnée. Un facteur M² bas correspond à une focalisation plus importante, une utilisation plus efficace de la puissance au sein du faisceau et une puissance effective potentielle du laser plus élevée.

Cependant, mesurer ce facteur M² n’est pas aussi simple que de mesurer le profil d’un faisceau au niveau d’un plan unique sur l’axe du laser. La norme ISO 11146 stipule que cinq mesures du rayon du faisceau doivent être effectuées à différents endroits le long de l’axe optique, tant dans le champ proche que dans le champ lointain.⁴ Il est possible de faire en sorte qu’un faisceau ressemble à un faisceau gaussien idéal dans un plan spécifique sans qu’il ne contienne aucun des modes TEM₀₀ (Figure 2). Même si la section transversale dans ce plan spécifique ressemble à une distribution gaussienne parfaite, le faisceau se propagera très différemment d’un faisceau gaussien et aura un angle de divergence plus important.⁵ De multiples mesures de rayon dans différents plans permettront de révéler rapidement la différence entre ce faisceau et un vrai faisceau gaussien. Le rayon mesuré (w(z)) du faisceau peut être mis en relation avec le waist de ce faisceau (w₀), la longueur d’onde (λ) et le facteur M² par l’équationpar l’équation⁶  :

Figure 2 : Cette section transversale du faisceau semble gaussienne à un plan spécifique même si elle ne contient aucun des modes TEM₀₀ ce qui illustre l’importance d’effectuer plusieurs mesures d’intensité le long de l’axe d’un laser pour déterminer son facteur M²

L’un des inconvénients de la caractérisation des faisceaux avec le facteur M² par rapport aux autres paramètres de qualité du faisceau est qu’elle met davantage l’accent sur les « ailes », c’est-à-dire les parties à faible densité de puissance du faisceau les plus éloignées du centre, ce qui la rend parfois mieux adaptée aux milieux universitaires qu’aux applications industrielles.

Produit des paramètres du faisceau

Le produit des paramètres du faisceau (ou BPP pour Beam Parameter Product) est une mesure permettant d’évaluer la qualité d’un faisceau laser. Il est défini comme étant le produit du rayon du faisceau à son waist par le demi-angle de divergence du faisceau. Il est généralement exprimé en mm mrad et il est lié au facteur M² par :

Puisque le BPP est directement proportionnel au facteur M², un produit des paramètres du faisceau élevé correspond à un faisceau de basse qualité. La valeur minimum du BPP est λ/π, qui ne peut être obtenue que dans le cas d’un faisceau gaussien idéal.

Le BPP est couramment utilisé pour caractériser les lasers à fibre ou à semi-conducteurs ayant un facteur M² élevé, ainsi que les systèmes diode-laser à fibre couplés pour déterminer la quantité de lumière qui peut être couplée dans une fibre.

Power in the Bucket

La puissance dans le godet (ou PIB pour Power in the Bucket) est une autre mesure permettant de définir la qualité du faisceau ; elle est souvent utilisée dans les systèmes laser de haute puissance et les applications de traitement des matériaux. La PIB décrit la quantité de puissance laser intégrée sur un « godet » spécifié, le plus souvent un spot d’un rayon spécifique à la surface du matériau traité. Bien que ce concept semble simple, la forme du godet en champ lointain doit être bien définie et les comparaisons avec les scénarios idéaux dépendent de la spécification de la forme idéale du faisceau laser en champ proche.
Bien qu’il n’existe pas de norme industrielle pour la définition exacte de la PIB, elle est le plus souvent indiquée comme une qualité de faisceau verticale ou horizontale⁷ :

De la même façon que pour le facteur M² et le BPP, une valeur de PIB faible correspond à un faisceau de haute qualité. La PIB peut être visualisée en traçant la fraction de puissance dans le « godet » défini en fonction de λ/D, où D est le diamètre du faisceau en champ proche (Figure 3). La qualité de faisceau verticale est la racine carrée du rapport entre la fraction de la puissance dans le godet d’un faisceau gaussien idéal et celle du faisceau réel à un λ/D donné, qui correspond à la dimension verticale du tracé. De la même façon, la qualité de faisceau horizontale est le rapport entre la valeur λ/D d’un faisceau gaussien idéal et celle du faisceau réel à une fraction de puissance dans le godet donnée, qui correspond à la dimension horizontale du tracé.

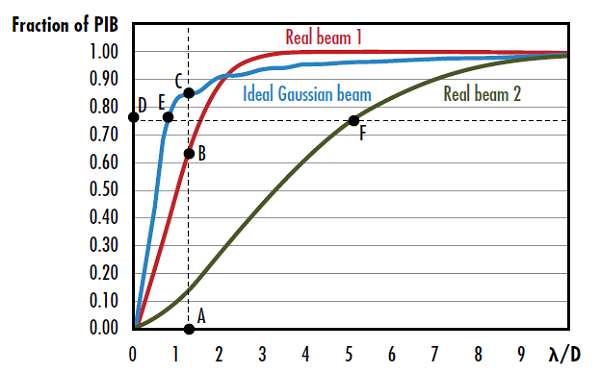
Figure 3 : La qualité de faisceau verticale du faisceau réel 1 est donnée par la racine carrée du rapport du segment AC sur le segment AB, et la qualité de faisceau horizontale du faisceau réel 2 est donnée par le rapport du segment DF sur le segment DE⁷

Faisceaux circulaires et faisceaux elliptiques

Lorsqu’on considère la forme d’un faisceau laser, il est important de déterminer si le laser produit un faisceau circulaire ou elliptique. Les faisceaux elliptiques peuvent être préjudiciables aux performances du système car ils ont une taille de spot focalisé plus importante que les faisceaux circulaires. Cette plus grande taille du spot entraîne une irradiance (flux d’énergie radiante par unité de surface) plus faible qu’un faisceau circulaire, qui à son tour peut nécessiter une puissance d’entrée plus élevée au laser. Les diodes laser à semi-conducteurs émettent des faisceaux de forme elliptique avec des angles de divergence différents dans les directions x et y en raison de la forme rectangulaire de leur région active (Figure 4). La diffraction est plus grande pour les petites ouvertures, donc la dimension plus courte de la région active produira un faisceau plus divergent et donnera un faisceau astigmatique. L’axe avec le plus grand angle de divergence est défini comme l’axe rapide, tandis que l’axe avec le plus petit angle de divergence est défini comme l’axe lent. Les lentilles cylindriques sont souvent utilisées pour circulariser les faisceaux elliptiques (Figure 5). Pour en savoir plus sur les lentilles cylindriques, consultez notre note d’application À considérer lors de l’Utilisation de Lentilles Cylindriques.

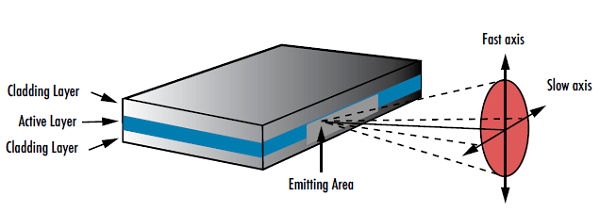
Figure 4 : La géométrie des diodes laser entraîne des faisceaux elliptiques présentant deux angles de divergence différents

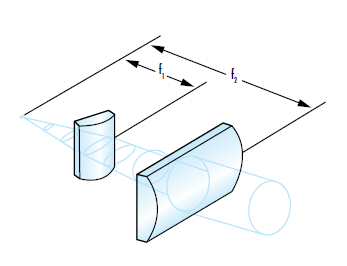
Figure 5 : Les lentilles cylindriques sont souvent utilisées pour circulariser un faisceau elliptique en agissant séparément sur les axes rapide et lent

Rapport de Strehl

Tout comme le facteur M² compare la performance réelle d’un laser à celle d’un faisceau idéal, le rapport de Strehl d’un système ou d’un composant optique compare sa performance réelle avec une version idéale. Le rapport de Strehl des optiques de focalisation, comme les lentilles sphériques et asphériques, est le rapport entre l’irradiation maximale du point focal de l’optique réelle d’une source ponctuelle et l’irradiation maximale idéale d’une optique théorique limitée par la diffraction (Figure 6).⁷ Un rapport de Strehl de 1 indiquerait qu’une optique est parfaite et sans aberration. La pratique industrielle courante considère qu’une lentille est « limitée par la diffraction » lorsque le rapport de Strehl est supérieur à 0,8.

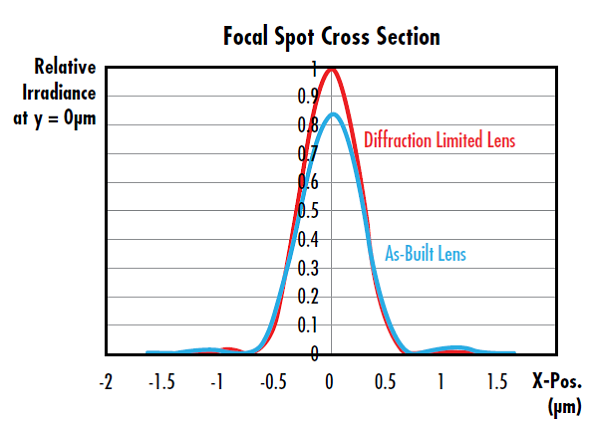
Figure 6 : Cette lentille présente un rapport de Strehl de 0,826, elle est donc considérée comme limitée par la diffraction car le rapport est supérieur à 0,8.

Le rapport de Strehl d’une optique est approximativement lié à l’erreur de front d’onde transmis de RMS par l'Équation 8 où S est le rapport de Strehl de l’optique et σ est l’erreur de front d’onde RMS de l’optique en ondes.⁸ Cette approximation est valable lorsque l’erreur de front d’onde est <0.2 ondes.

Pour en savoir plus sur la manière dont l’irrégularité de la surface d’une optique affecte son rapport de Strehl, consultez notre note d’application Rapport de Strehl et irrégularité des asphères/a> .

Références

1. International Organization for Standardization. (2005). Lasers and laser-related equipment – Test methods for laser beam widths, divergence angles and beam propagation ratios (ISO 11146).
2. A. E. Siegman, “New developments in laser resonators”, Proc. SPIE 1224, 2 (1990)
3. Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
4. International Organization for Standardization. (2005). Lasers and laser-related equipment — Test methods for laser beam widths, divergence angles and beam propagation ratios — Part 1: Stigmatic and simple astigmatic beams (ISO 11146-1:2005).
5. A. Siegman, “’Non-Gaussian’ Beam”, OSA Annual Meeting, Long Beach, CA (1997)
6. Hofer, Lucas. “M² Measurement.” DataRay Inc., 12 Apr. 2016, www.dataray.com/blog-m2-measurement.html.
7. Strehl, Karl W. A. “Theory of the telescope due to the diffraction of light,” Leipzig, 1894.
8. Mahajan, Virendra N. "Strehl ratio for primary aberrations in terms of their aberration variance." JOSA 73.6 (1983): 860-861.

Section précédente Section suivante