Rapport de Strehl et irrégularité des asphères

Tous les systèmes optiques présentent une limite théorique de performances, appelée limite de diffraction. Le rapport de Strehl est une spécification permettant de comparer les performances réelles d’un système optique à ses performances limitées par la diffraction. Pour les lentilles asphériques et d’autres composants optiques de focalisation, le rapport de Strehl est défini comme étant le rapport entre l’irradiance maximale du point focal de l’optique fabriquée et l’irradiance maximale limitée par la diffraction (Figure 1).¹ Les différentes techniques de fabrication des lentilles asphériques entraînent des erreurs de surface uniques qui affectent différemment le rapport de Strehl. Il est important de comprendre ces effets afin de spécifier correctement les asphères, d’éviter toute spécification abusive pouvant s’avérer inutile et coûteuse, tout en s’assurant que les spécifications souhaitées sont appliquées. Cela devient de plus en plus crucial pour les asphères rapides avec des petits rapports f/#, et affecte davantage les asphères fabriquées par le meulage et le polissage conventionnels que celles fabriquées par d’autres méthodes. Le seuil standard de l’industrie pour classer une lentille comme « limitée par la diffraction » est un rapport de Strehl supérieur à 0.8.

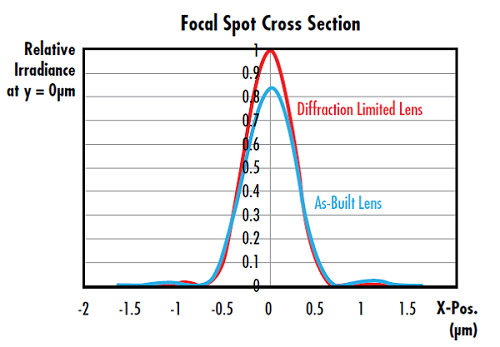
Figure 1 : Courbe de section transversale de l’irradiance du point focal d’une lentille asphérique f/2 de 25 mm de diamètre à 588 nm. Les lentilles, telles qu’elles sont fabriquées, présentent un rapport de Strehl de 0,826 correspondant au critère de limite de diffraction

Le rapport de Strehl peut aussi être mis en relation avec l’erreur de front d’onde transmis RMS à l’aide de l’approximation suivante, dans laquelle $ \small{\sigma} $ représente l’erreur de front d’onde RMS en ondes.² Cette approximation est valide pour les valeurs d’erreur de front d’onde transmis <0.2 ondes.³

Impact de l’irrégularité de surface sur le rapport de Strehl

Le rapport de Strehl d’un composant optique dépend en grande partie de son irrégularité de surface ou de la déviation de la surface optique par rapport à sa forme nominale ; l’irrégularité de surface résulte de la méthode de fabrication utilisée. Les composants optiques sphériques sont généralement polis à l’aide d’un outil surdimensionné qui provoque de faibles erreurs de fréquence spatiale sur la surface optique. Pour fabriquer des lentilles asphériques, on utilise par contre généralement le meulage et le polissage de sous-ouverture, ce qui crée une structure à l’irrégularité plus complexe. Comprendre la relation entre une irrégularité de surface spécifiée et sa structure sous-jacente permet de mieux appréhender les performances d’une lentille et le rapport de Strehl qui en résulte.

Par exemple, prenons l’impact de la fréquence spatiale. Lorsque l’irrégularité de surface est modélisée comme une fonction cosinus à symétrie de rotation, nous pouvons explorer le rapport de Strehl résultant en fonction de l’irrégularité de surface RMS pour une variété de périodes cosinus (Figure 2 et Figure 3).

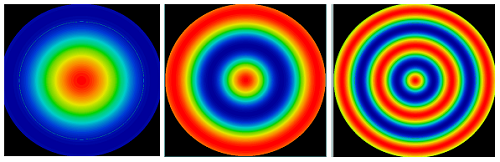
Figure 2 : Les erreurs typiques d’irrégularité de surface dans la fabrication des lentilles asphériques suivent les modèles de cosinus, comme ces cartes d’irrégularité du cosinus radial sur une surface asphérique f/2 de 25 mm de diamètre. Les périodes du cosinus de gauche à droite sont de 20 mm, 10 mm et 5 mm

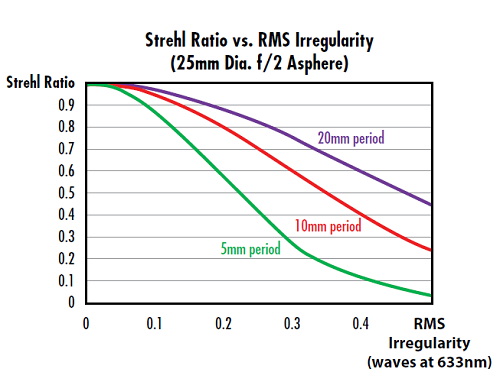
Figure 3 : Pour une irrégularité de surface RMS particulière, plus les périodes de cosinus sur l’ouverture de l’asphère sont nombreuses, plus le rapport de Strehl est faible

Ici, le facteur clé n’est pas la période du cosinus en mm, mais le nombre de périodes sur l’ouverture de la lentille. Pour un outil de sous-ouverture donné utilisé dans la fabrication de l’asphère, les asphères de petit diamètre auront une dégradation du rapport de Strehl inférieure à celle des asphères de grand diamètre.

L’impact de l’irrégularité de surface sur le rapport de Strehl dépend aussi du f/# de la lentille. En règle générale, les asphères plus rapides, ou les asphères avec des f/# plus petits, ont une plus grande sensibilité à l’impact de l’irrégularité de surface sur le ratio de Strehl. Par exemple, la Figure 4 compare une lentille f/2 à une lentille f/0,75 (toutes deux de 25 mm de diamètre), et on observe une dégradation plus importante du rapport de Strehl pour les lentilles les plus rapides par rapport aux lentilles les plus lentes à une période cosinus donnée.

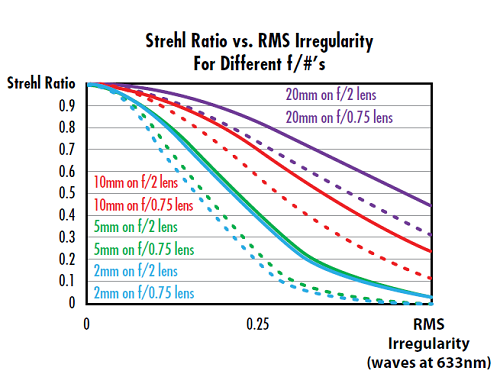
Figure 4 : La comparaison des lignes pointillées avec les lignes continues montre qu’une asphère plus rapide (f/# plus petit) a une dégradation plus importante qu’une asphère plus lente (f/# plus grand) sur une période cosinus donnée

Densité spectrale de puissance et pente d’irrégularité

D’après les exemples ci-dessus, le contenu en fréquences spatiales des cartes d’irrégularités a clairement un impact sur le rapport de Strehl de la lentille. En plus de l’irrégularité PV ou RMS, des spécifications supplémentaires peuvent être demandées pour cibler ces fréquences spatiales.

Une spécification utilisée pour évaluer directement les fréquences spatiales est appelée densité spectrale de puissance, ou DSP.⁴ La DSP évalue l’irrégularité de la surface en fonction de la fréquence spatiale et peut être utilisée de manière ciblée pour limiter la contribution d’une gamme de fréquences spatiales. La DSP peut également être utilisée pour contraindre toutes les fréquences spatiales simultanément.

Une méthode plus simple, mais efficace, pour réduire les fréquences spatiales plus élevées dans l’irrégularité consiste à contraindre la pente des fonctions cosinus composant la carte d’irrégularité de surface, en plus de la valeur PV. Pour une limite d’irrégularité PV donnée, des pentes plus élevées sont associées à des fréquences spatiales plus élevées sur la surface (Figure 5). SLa pente est souvent exprimée en termes de valeur de pente RMS maximale, ce qui constitue une évaluation plus complète de la surface de la lentille qu’une simple exigence de pente maximale.⁵

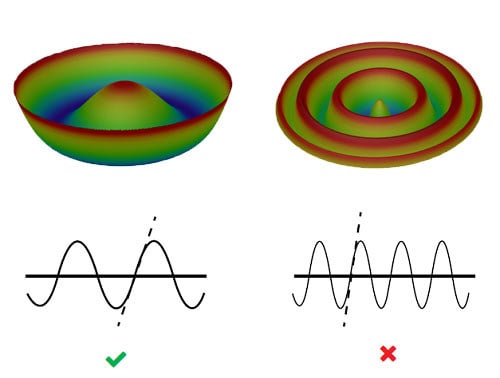
Figure 5 : Si une spécification de pente maximale est spécifiée pour la carte d’irrégularité de surface, cela crée un seuil permettant de réduire l’impact d’un contenu de fréquence spatiale plus élevé sur la surface

La fréquence spatiale de l’irrégularité de surface a un impact significatif sur le rapport de Strehl et les performances de l’asphère. Plus la période est courte, plus la dégradation du rapport de Strehl est importante pour une irrégularité de surface donnée. La forme de la carte d’irrégularité de la surface de la lentille est nécessaire pour comprendre l’impact réel de cette irrégularité sur sa performance, et pas seulement une spécification d’irrégularité en soi.⁶ Des f/# plus petits entraînent également une dégradation plus importante.

Références

1. Strehl, Karl W. A. “Theory of the telescope due to the diffraction of light,” Leipzig, 1894.
2. Mahajan, Virendra N. "Strehl ratio for primary aberrations in terms of their aberration variance." JOSA 73.6 (1983): 860-861.
3. Smith, Warren J. Modern Optical Engineering. 4th ed., McGraw-Hill Education, 2007.
4. Lawson, Janice K., et al. "Specification of optical components using the power spectral density function." Optical Manufacturing and Testing. Vol. 2536. International Society for Optics and Photonics, 1995.
5. Messelink, Wilhelmus A., et al., "Mid-spatial frequency errors of mass-produced aspheres," Proc. SPIE 10829, Fifth European Seminar on Precision Optics Manufacturing, 7 Aug. 2018, doi:10.1117/12.2318663.
6. Kasunic, Keith J., Laser Systems Engineering, SPIE Press, 2016. (ISBN 9781510604278)

Section précédente Section suivante