Conseils pour concevoir des lentilles et assemblages en vue d’une fabrication optimale

Une conception réussie d'une lentille ne se limite pas à la création d'un modèle fonctionnel, mais comprend également la fabrication, l'assemblage, les essais et la mise en œuvre. Il arrive qu'une lentille semble avoir été conçue avec succès, mais qu'elle échoue dans l'une des phases ultérieures de fabrication, d'assemblage ou d'essai. C'est pourquoi il est impératif de reconnaître les nuances de la fabrication optique, en accordant une attention particulière à l'hypothèse statistique des modèles et à l'aspect pratique de la fabrication. Les concepteurs doivent tenir compte de la géométrie de la lentille, de la configuration de l'assemblage et des modèles de tolérances lorsqu'ils créent une optique à partir de zéro.

Considérations géométriques

Les logiciels de conception numérisent le processus de planification optique et offrent des outils qui facilitent la procédure détaillée et fastidieuse. Toutefois, il faut savoir que la plupart des logiciels optiques n'avertissent pas toujours l'utilisateur lorsqu’il crée des solutions physiquement impossibles ou difficiles à fabriquer, et ne l'empêchent pas de le faire. N'oubliez pas que le logiciel optique n'est qu'un outil et que l'utilisateur doit accorder une attention particulière à l'examen des résultats.

Une technique courante utilisée par les fabricants d'optiques pour usiner le verre ou d'autres matériaux selon les spécifications finales consiste à surdimensionner le diamètre de la lentille au début du processus de fabrication. Anticipant la nécessité de surdimensionner le diamètre de la lentille, les concepteurs doivent s'assurer que l'épaisseur du bord n'est pas trop faible ni trop tranchante, de sorte que le bord serait susceptible d'être endommagé. Il est conseillé de maintenir l'épaisseur des bords au-dessus d’environ 0,7 mm, à un diamètre supérieur de 1 mm au diamètre final prévu pour la lentille.

Le facteur de Karow ou facteur Z, qui mesure la capacité d'une lentille à se centrer automatiquement entre des mandrins à mors, est donné par la formule suivante :

D₁, D₂ sont les diamètres du mandrin à mors (généralement égal au diamètre de l'ouverture utile de la lentille). R₁, R₂ sont les rayons de courbure de la première et de la deuxième surface. Les surfaces convexes et concaves ont respectivement des rayons positifs et négatifs (Figure 1).

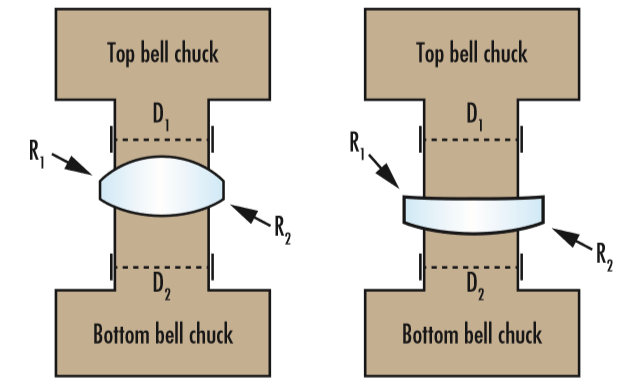
Figure 1 : Le facteur de Karow de la lentille gauche (Z = 2,5) est supérieur à celui de la lentille droite (Z = 0,4). Ainsi, la lentille gauche serait plus facile à centrer par le biais d'un serrage auto-centrant du mandrin, tandis que la droite serait plus difficile à centrer.

Les lentilles dont le facteur de Karow est supérieur à 0,56 se centreront automatiquement par le biais d'un centrage automatique ; ceux dont le facteur de Karow est inférieur à 0,56 ne se centreront pas automatiquement et devront être centrés manuellement. Il s'agit d'un processus qui prend beaucoup de temps et qui est donc plus coûteux. Les lentilles dont les rayons sont presque concentriques sont difficiles à centrer car une grande quantité de matériau doit être enlevée pour corriger le décentrement relatif de surface à surface. Pour garantir le centrage d'une lentille, la concentricité (Δr) doit être supérieure à 2 mm en règle générale :

Où CT est l'épaisseur au centre de la lentille (Figure 2).

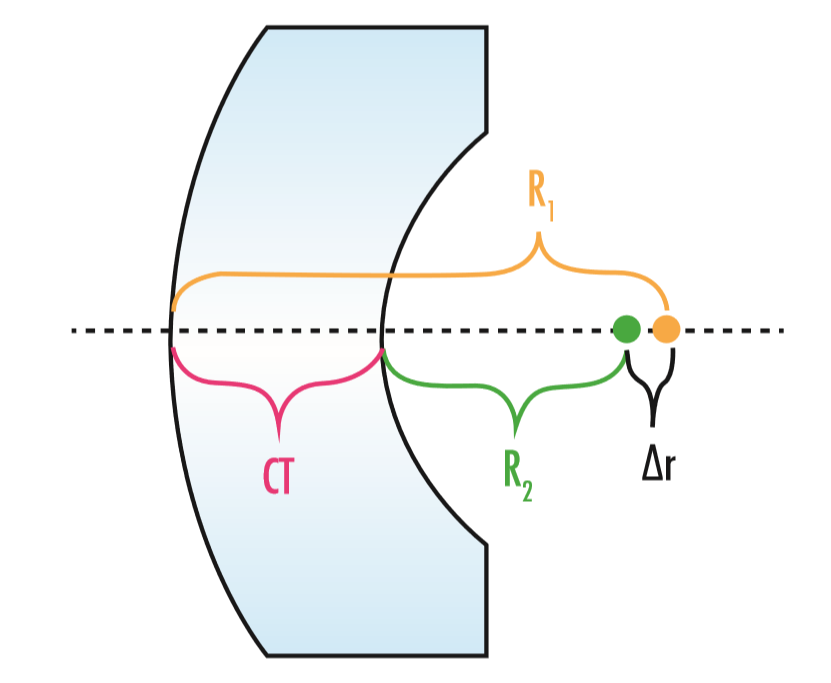
Figure 2 : Cette lentille ménisque a des rayons presque concentriques. Veillez à ce que |∆r| soit supérieur à 2 mm afin que la lentille puisse être centrée.

Les lentilles à surface hémisphérique (rayons de courbure inférieurs ou égaux à 0,7 fois le diamètre) ou quasi plane (un sag égal ou inférieur à 100 μm) doivent également être évitées si possible, car cela est également difficile à fabriquer.

Méthodes et hypothèses de tolérancement

Au cours de la dernière décennie, la modélisation statistique est devenue un outil de plus en plus utilisé dans le secteur de l'optique. La simulation de Monte Carlo est la méthode analytique la plus courante pour modéliser la probabilité de performance d'un système optique. Il est donc important de comprendre les modèles statistiques et les distributions de probabilité qui peuvent être utilisés pour contrôler les tolérances des spécifications.

Comme pour le diamètre d'une lentille, l'épaisseur au centre est généralement maintenue intentionnellement pendant les premières étapes de la fabrication. Le fabricant dispose ainsi d'une plus grande marge de tolérance pour affiner d'autres dimensions ou spécifications, telles que la précision ou la qualité de la surface, qui réduisent naturellement la dimension de l'épaisseur au centre. Pour cette raison, la distribution de l'épaisseur au centre d'un lot de lentilles sera probablement biaisée vers le côté supérieur de la plage de tolérance (Figure 3).

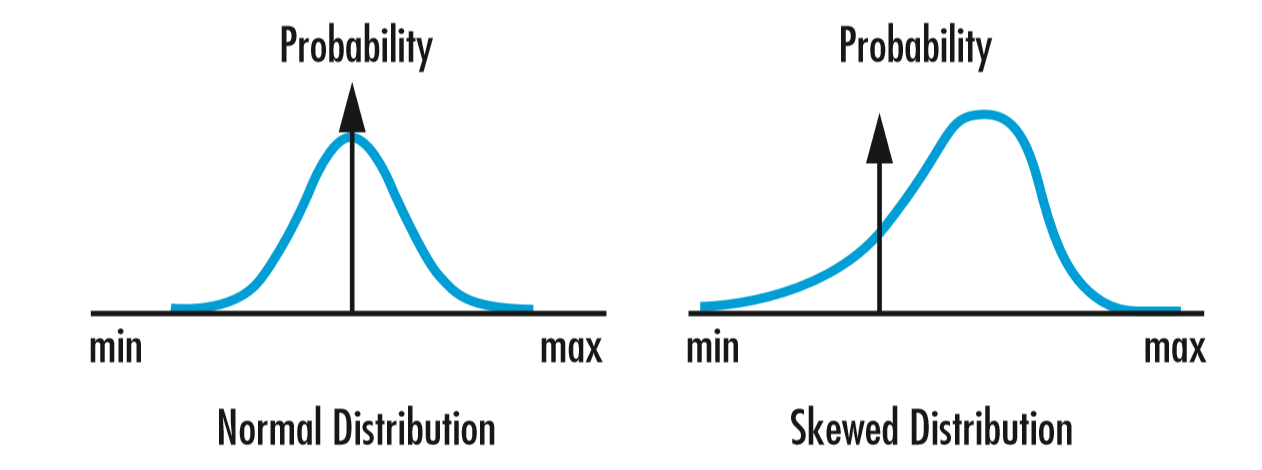
Figure 3 : Une lentille est souvent surdimensionnée pour permettre des corrections en aval, ce qui fausse la distribution de la valeur des dimensions telles que l'épaisseur au centre ou le diamètre au sein d'un lot donné.

Au cours d'une analyse de Monte Carlo, on suppose souvent à tort que la distribution de l'épaisseur au centre suit une distribution normale symétrique, sans asymétrie ni aplatissement. En réalité, un certain nombre de facteurs influencent la forme de la distribution, notamment le nombre de lentilles dans le lot, le processus de fabrication (par exemple, fraisage au diamant ou processus par lots) et le style d'un technicien particulier.  Une analyse de sensibilité peut aider à déterminer les facteurs qui ont le plus d'impact sur la conception et aider les concepteurs à établir des priorités.

Modélisation de l'irrégularité de la surface

La modélisation des irrégularités de surface (SI) peut être aussi simple ou complexe que nécessaire. Deux modèles SI simplifiés couramment utilisés consistent à adapter une surface à une combinaison 50/50 d'aberration sphérique et d'astigmatisme ou à un astigmatisme à 100%. Il est vivement recommandé de tenir compte de la coma, du trèfle et d'autres effets d'ordre supérieur pour les assemblages de lentilles comportant un grand nombre d'éléments ou pour les systèmes optiquement sensibles, car les modèles SI simplifiés ne reproduisent souvent pas suffisamment l'erreur ou l'irrégularité du front d'onde dans le système. L'ajustement des cartes d'irrégularités de surface réelles aux coefficients de Zernike est une méthode de modélisation beaucoup plus précise, et la plupart des logiciels de conception intègrent cette fonctionnalité de tolérancement (Figure 4).

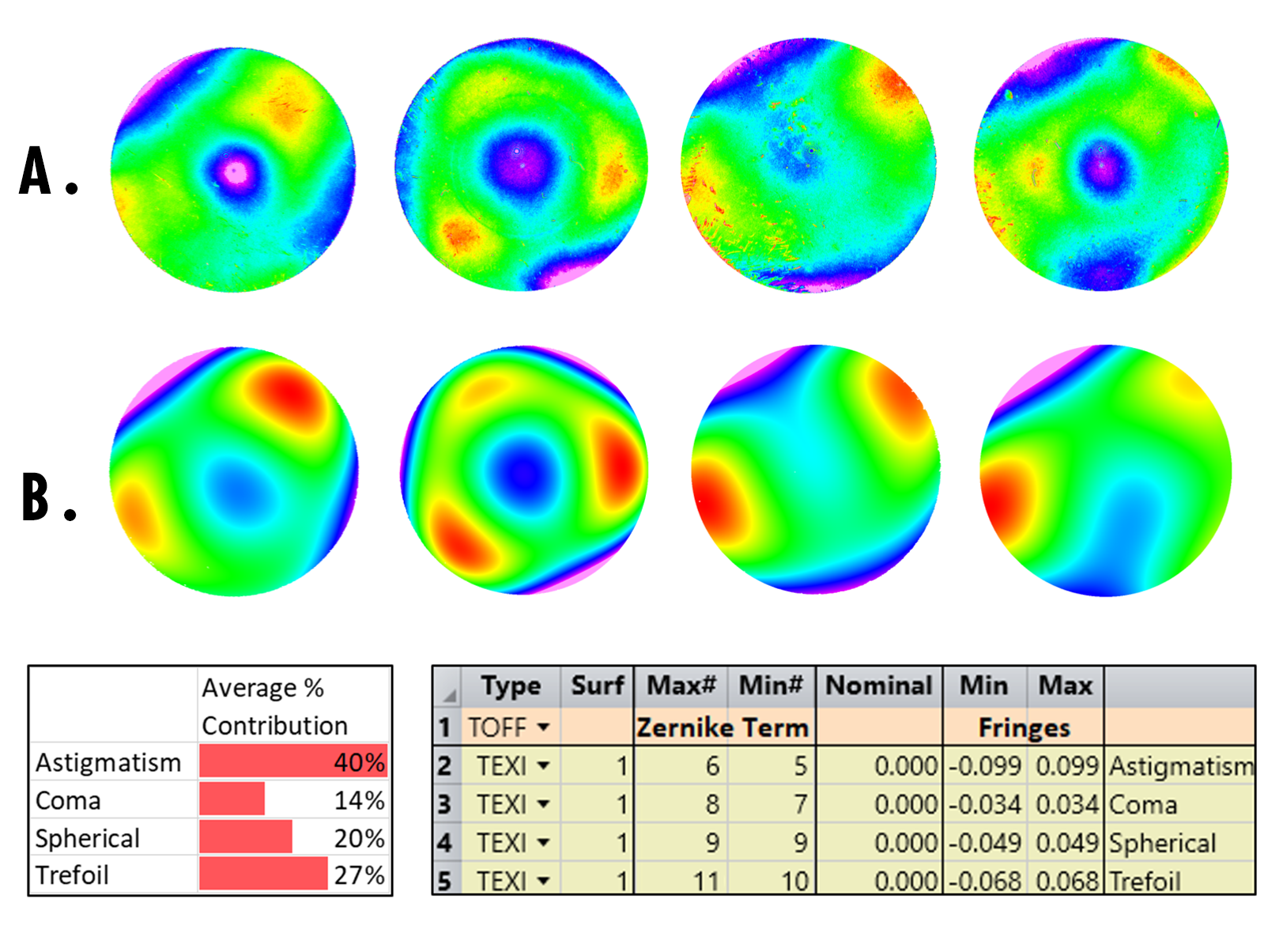
Figure 4 : A. Quatre motifs d'irrégularité de surface basés sur les coefficients de Zernike 5 à 11. B. Modèles approximatifs adaptés aux coefficients de Zernike simulés dans Zemax OpticStudio.

Cette méthode de modélisation nécessite des mesures de la surface des lentilles, ce qui entraîne un surcroît de temps et d'efforts, et donc de dépenses. Il est également important de comprendre exactement quel schéma de Zernike un logiciel de conception de lentilles utilise. Il existe de nombreux schémas de Zernike, tous incompatibles entre eux, avec des expressions et des coefficients légèrement différents. Les schémas de Zernike standard (ou Noll) et de Zernike Fringe sont deux schémas de Zernike souvent utilisés dans la conception de lentilles.

Empilages de systèmes assemblés

Les fabricants assemblent des lentilles et doivent être en mesure de garantir que les groupes de lentilles restent conformes aux spécifications, même en présence d'effets d'inclinaison et de décentrement. Les assemblages optiques requièrent une attention supplémentaire pour le calage et l'inclinaison des éléments individuels ainsi que pour les empilements au niveau du système, car les éléments et les entretoises se poussent les uns contre les autres, tout en étant soumis aux limites du diamètre intérieur du barillet. Les modèles d'empilement doivent tenter d'accumuler les effets d'inclinaison et de décentrement, tout en gardant les éléments ancrés à l'axe optique, pour plus de précision. Pour modéliser un système, il faut s'assurer que chaque itération de Monte Carlo est configurée avec l'empilement correct d'inclinaisons d'éléments en fonction de la disposition des éléments dans l'assemblage (Figure 5).

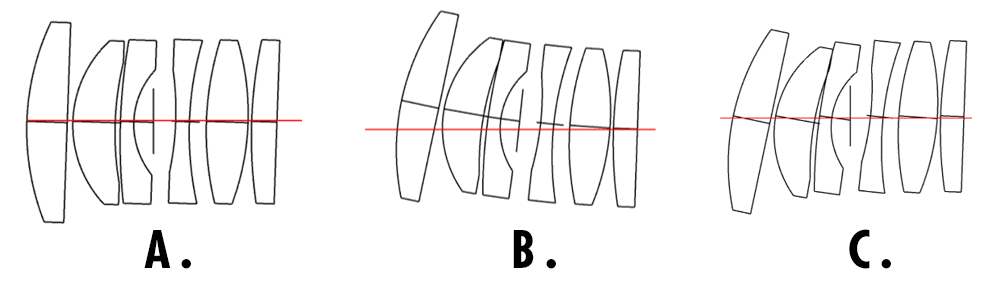
Figure 5 : Trois approches de l'inclinaison des lentilles dans un assemblage de type « drop-together ». Tous les éléments sont inclinés de 2° dans la même direction pour illustrer les différences. A. Les inclinaisons sont modélisées de manière indépendante. B. Les inclinaisons et les décentrements sont cumulés dans l'ordre d'assemblage. C. Les inclinaisons sont cumulées dans l'ordre d'assemblage, sans décentrement supplémentaire ; ce mouvement est appelé cisaillement.

Le basculement (« Roll ») et le décentrement d'un élément peuvent affecter les éléments suivants dans le barillet. Les éléments connectés seront « couplés » à un seul élément basculant et se déplaceront ensemble. Seuls les éléments dont la surface arrière est convexe et qui sont en contact avec des entretoises ont un décentrement couplé. Les éléments avec des anneaux ou des surfaces planes reposant sur une entretoise peuvent se déplacer indépendamment (sans être couplés) à partir d'un élément initialement décentré (Figure 6).

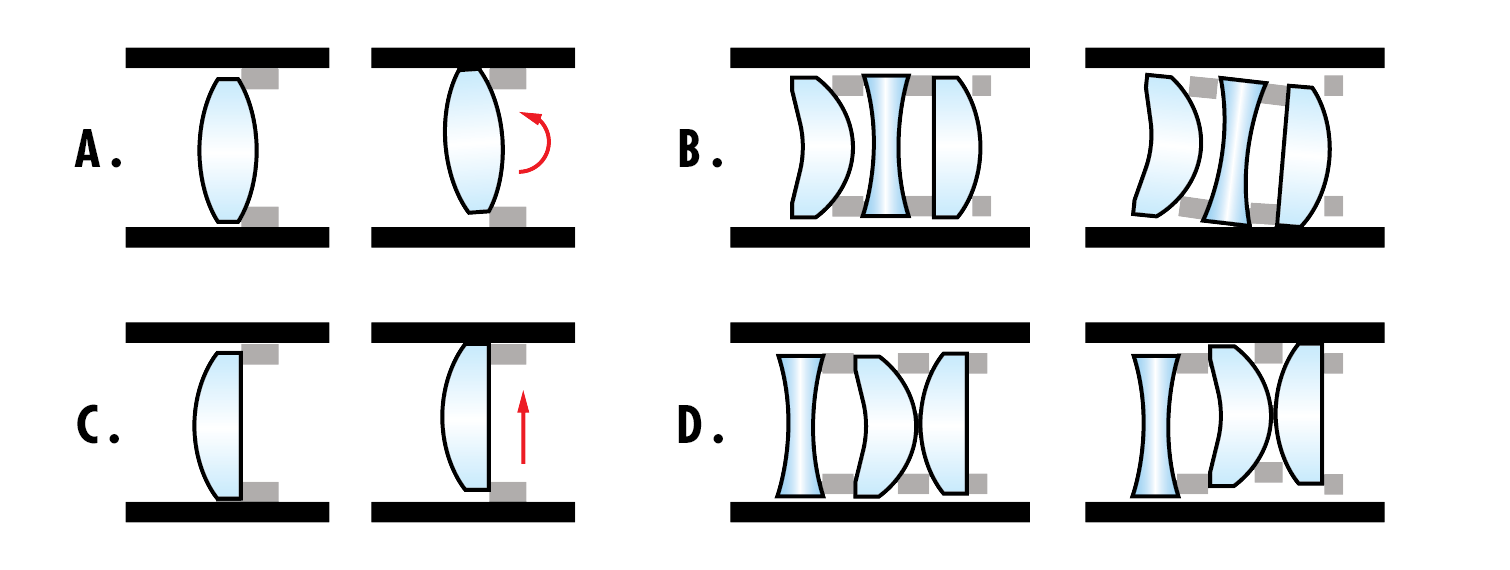
Figure 6 : A. Mouvement de basculement (« Roll ») d'un élément de lentille. B. Mouvement de basculement (« Roll ») couplé. C. Mouvement de décentrement d'un élément de lentille. D. Mouvement de décentrement couplé.

En fonction de l'application pour laquelle l'assemblage est conçu, le basculement et le décentrement peuvent avoir une incidence importante – ou nulle – sur les performances. Le tolérancement des composants peut toutefois fournir des informations précieuses sur le processus d'assemblage possible et peut aider à trouver des méthodes alternatives, telles que le regroupement de différents éléments en sous-cellules ou l'installation d'éléments dans un ordre différent, si d'autres solutions sont nécessaires.

En simplifiant à l'extrême les modèles de tolérance et les conceptions, on risque de négliger d'éventuels problèmes de fabrication, et ce faisant, on augmente la probabilité que les conceptions nécessitent des révisions ou des itérations supplémentaires avec des niveaux de complexité accrus. En outre, il se peut que les assemblages soient fabricables mais donnent des produits médiocres, non robustes, qui ne répondent pas aux spécifications de la conception. De tels cas prolongent inévitablement la durée d'un projet et en augmentent le coût. L'amélioration de la précision du modèle du système et l'utilisation de méthodes de tolérancement haute fidélité dès le début de la conception nécessiteront des efforts supplémentaires au départ, mais permettront de réduire les erreurs coûteuses et de gagner du temps en fin de compte.

Références

1. H.H. Karow (2004). Fabrication Methods for Precision Optics. J. Wiley & Sons, Inc.
2. R. Bean (April 28, 2017). How Companies Say They’re Using Big Data. Harvard Business Review, https://hbr.org/2017/04/how-companies-say-theyre-using-big-data.
3. M.I. Kaufman et al. (September 19, 2014). Statistical distributions from lens manufacturing data, Proc SPIE 9195, Optical System Alignment, Tolerancing, and Verification VIII, 919507 ; https://doi.org/10.1117/12.2064582.
4. Zemax LLC (2018). Zemax OpticStudio 18.4 User Manual. Kirkland, Wash.
5. Synopsys (2018). CODE V Tolerancing Reference Manual. Mountain View, Calif.