Modes de résonateurs laser

Cela correspond à la section 4.1 du Guide des Ressources en Optique Laser.

La forme d'un faisceau laser est déterminée par la cavité du résonateur, un miroir optique laser, dans lequel la lumière laser est amplifiée dans un milieu de gain. Les résonateurs laser sont généralement formés en utilisant des miroirs diélectriques hautement réfléchissants ou un cristal monolithique qui utilise la réflexion interne totale pour empêcher la lumière de s'échapper (Figure 1). Voici une liste des géométries de résonateurs laser les plus courantes¹ :

Résonateur plan parallèle : deux miroirs plats séparés par une distance égale à un multiple entier de la moitié de la longueur d’onde de l’émission laser
Résonateur concentrique : deux miroirs sphériques ayant le même rayon de courbure et des centres de courbure coïncidents
Résonateur confocal : deux miroirs sphériques ayant le même rayon de courbure et des points focaux coïncidents
Résonateur en anneau : anneau composé de plus de deux réflecteurs où le trajet total en boucle fermée de la lumière réfléchie est égal à un multiple entier de la moitié de la longueur d’onde de l’émission laser

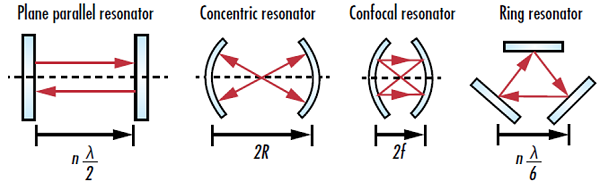
Figure 1 : Quatre types courants de géométries de résonateurs laser où n est une valeur entière, λ est la longueur d’onde de l’émission laser, R est le rayon de courbure d’un miroir courbe et f est la longueur focale d’un miroir courbe

Les cavités des résonateurs sont « stables » si la lumière réfléchie reste à l’intérieur de ces cavités, même lorsque le nombre de réflexions est proche de l’infini (Figure 2). ). Dans ce cas, la seule façon pour la lumière de quitter la cavité est de passer par un miroir partiellement réfléchissant. D’autre part, les cavités des résonateurs sont considérées comme « instables » si la lumière réfléchie diverge continuellement lorsque le nombre de réflexions approche l’infini. Lorsque cela se produit, le faisceau grandit jusqu’à devenir plus grand que les réflecteurs et s’échapper du système. Les résonateurs stables sont souvent utilisés avec des lasers présentant des puissances allant jusqu’à 2 kW pour obtenir un gain élevé et améliorer la directivité. Les résonateurs instables sont généralement utilisés avec des lasers à haute puissance pour réduire le risque d’endommager les réflecteurs.¹

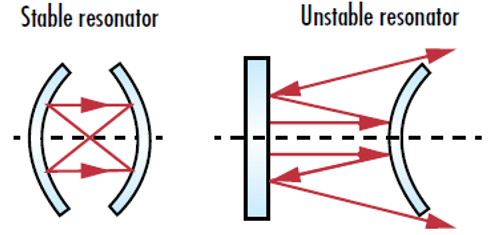
Figure 2 : Les résonateurs laser stables maintiennent tous les faisceaux réfléchis dans les limites de la cavité, tandis que les résonateurs instables entraînent la dispersion de la lumière réfléchie jusqu’à ce qu’elle s’échappe de la cavité

La longueur du trajet de la cavité du résonateur détermine les modes de résonateurs longitudinaux, ou les distributions de champs électriques qui provoquent une onde stationnaire dans la cavité. Les modes d’un faisceau lui procurent sa forme. Ces modes conservent leur profil d’amplitude et se reproduisent après avoir effectué un trajet en boucle fermée à l’intérieur du résonateur (hormis la perte potentielle de puissance due à la perte dans la cavité). Pour qu’un mode résonant se produise, il doit également subir un changement de phase égal à un multiple entier de 2π sur un trajet en boucle fermée Figure 3).

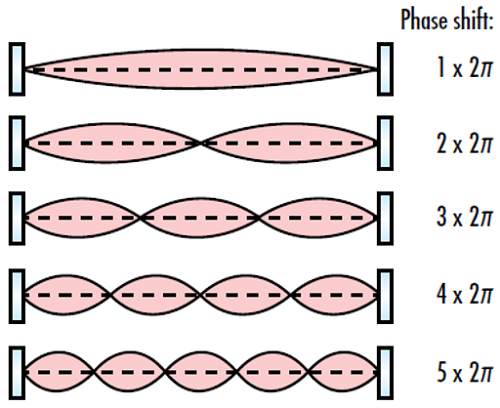
Figure 3 : Le changement de phase d’une boucle complète dans un résonateur optique doit représenter un multiple entier de 2π afin qu’un mode résonant se produise

Les modes de résonateurs laser les plus simples sont les modes Hermite-Gaussiens, également connus sous le nom de modes électromagnétiques transversaux (TEM_nm), dans lesquels le profil du champ électrique peut être estimé par le produit d’une fonction gaussienne par un polynôme Hermite²:

\begin{align}
E_{nm} \! \left(x, y, z \right) = & \, E_0 \frac{w_0}{w \! \left( z \right)} \, \cdot \, H_{n} \left( \sqrt{2} \frac{x}{w \! \left( z \right)} \right) \\
& \cdot \exp{\left( -\frac{x^2}{w \! \left( z \right) ^2} \right)} \, \cdot \, H_m \left( \sqrt{2} \frac{y}{w \! \left( z \right)} \right) \cdot \exp{\left( -\frac{y^2}{w \! \left( z \right) ^2} \right)} \\
& \cdot \, \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right)}{2 R \! \left( z \right) } \right] \Bigg]}
\end{align}

\begin{align} E_{nm} \! \left(x, y, z \right) = & \, E_0 \frac{w_0}{w \! \left( z \right)} \, \cdot \, H_{n} \left( \sqrt{2} \frac{x}{w \! \left( z \right)} \right) \\ & \cdot \exp{\left( -\frac{x^2}{w \! \left( z \right) ^2} \right)} \, \cdot \, H_m \left( \sqrt{2} \frac{y}{w \! \left( z \right)} \right) \cdot \exp{\left( -\frac{y^2}{w \! \left( z \right) ^2} \right)} \\ & \cdot \, \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right)}{2 R \! \left( z \right) } \right] \Bigg]} \end{align}

\begin{align} E_{nm} \! \left(x, y, z \right) = & \, E_0 \cdot H_n \cdot H_m \frac{w_0 \, x \, y}{\left[ w \! \left( z \right) \right]^3} \cdot \exp{\left[ - \left( \frac{x}{w \! \left( z \right)} \right)^2 \right]} \cdot \exp{\left[ - \left( \frac{y}{w \! \left( z \right)} \right)^2 \right]} \\ & \cdot \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right) }{2 R \! \left( z \right)} \right] \Bigg]} \end{align}

E₀ est le champ maximum
x et y sont les axes qui définissent une section transversale du faisceau
z est l’axe de propagation
w₀ est le waist du faisceau
w(z) est le rayon du faisceau à une valeur z donnée
H_n(x) et H_m(x) sont le polynôme Hermite avec les indices entiers non négatifs n et m
k est le nombre d’onde (k=2π/λ)
z_R est la longueur de Rayleigh
R(z) est le rayon de courbure du front d’onde

Les entiers n et m déterminent la forme du faisceau dans les directions x et y, respectivement. Un faisceau gaussien idéal est défini par le mode TEM₀₀, qui se produit lorsque n et m sont tous deux égaux à 0 (Figure 4). Pour plus d’informations sur les faisceaux gaussiens, veuillez consulter notre note d’application Propagation d’un faisceau gaussien. Toutes les autres valeurs de n et m produisent des modes de résonateurs plus compliqués.³ Dans la Figure 5, les géométries à section transversale des modes Hermite-Gaussiens d’ordre inférieur avec des valeurs n et m allant de 0 à 3 sont indiquées.

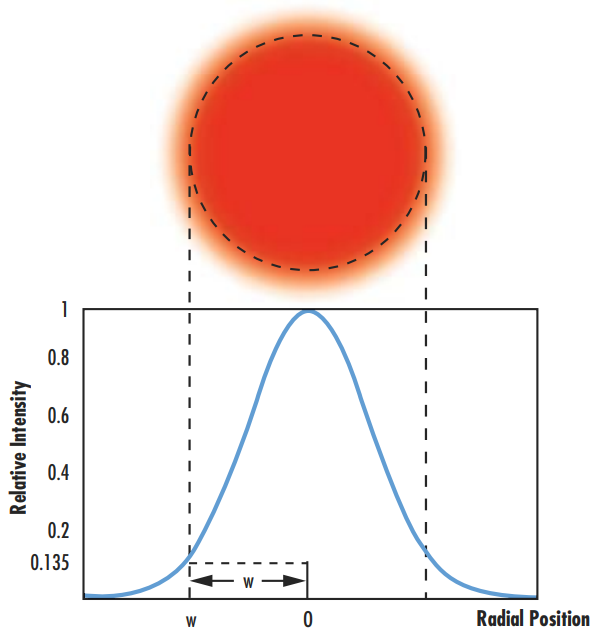
Figure 4 : Le mode de résonateur Hermite-Gaussien TEM00 correspond à un faisceau gaussien parfait

Figure 4 : Le mode de résonateur Hermite-Gaussien TEM₀₀ correspond à un faisceau gaussien parfait

Figure 5 : CSections transversales des modes de résonateurs Hermite-Gaussiens d’ordre inférieur avec des valeurs n et m allant de 0 à 3.

Figure 5 : Sections transversales des modes de résonateurs Hermite-Gaussiens d’ordre inférieur avec des valeurs n et m allant de 0 à 3.

Références

“Section 2.6: Various Laser Resonators.” Advanced Manufacturing Laboratory, Columbia Engineering, www.aml.engineering.columbia.edu/ntm/level2/ch02/html/l2c02s06.html.
Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
Paschotta Rüdiger. Field Guide to Lasers. SPIE Press, 2008.

Section précédente Section suivante

More Resources