Propagation des faisceaux gaussiens
Cela correspond à la Section 2.1 du Guide des Ressources en Optique Laser.
Dans de nombreuses applications d'optique laser, le faisceau laser est supposé être gaussien avec un profil d'irradiance suivant une distribution gaussienne idéale. Les faisceaux laser réels présentent tous une certaine déviation par rapport au comportement gaussien idéal. Le facteur M2, aussi connu sous le nom de facteur de qualité de faisceau, compare la performance d'un faisceau laser réel à celui d'un faisceau gaussien limité par la diffraction.1 Les profils d'irradiance gaussiens sont symétriques autour du centre du faisceau et diminuent à mesure qu'augmente la distance du centre du faisceau perpendiculairement à la direction de la propagation (Figure 1). Cette distribution est décrite au moyen de l'équation 12:
Dans l'équation 1, I0 désigne le pic d'irradiance au centre du faisceau, r est la distance radiale par rapport à l'axe, w(z) est le rayon du faisceau laser, où l'irradiance est 1/e2 (13.5%) de I0étant la distance propagée par rapport au plan où le front d'onde est plan et P la puissance totale du faisceau.

Figure 1 : le waist (aussi appelé col) d'un faisceau gaussien est défini comme l'endroit où l'irradiance es 1/e2 (13.5%) de sa valeur maximale
Cependant, ce profil d'irradiance n'est pas constant à mesure que le faisceau se propage à travers l'espace, d'où la dépendance de w(z) à z. En raison de la diffraction, un faisceau gaussien convergera et divergera par rapport à une zone appelée waist du faisceau (w0), qui correspond à l'endroit où le diamètre est à son minimum. Le faisceau converge et diverge de manière égale des deux côtés du waist du faisceau, selon un angle de divergence θ (Figure 2). Le waist du faisceau et l'angle de divergence sont tous deux mesurés par rapport à l'axe et leur relation est visible dans l'équation et l'équation 32:
Dans les équations ci-dessus, λ est la longueur d'onde du laser et θ est une approximation de champ lointain. Aussi, θ ne représente pas la divergence du faisceau de manière précise près du waist du faisceau, mais devient de plus en plus précis à mesure que la distance du waist du faisceau augmente. Comme l'indique l'équation 3, un faible waist de faisceau entraîne un angle de divergence plus grand, tandis qu'un waist de faisceau élevé entraîne un angle de divergence plus faible (ou un faisceau collimaté). Cela explique pourquoi les expanseurs de faisceau peuvent réduire la divergence du faisceau en augmentant le diamètre du faisceau.
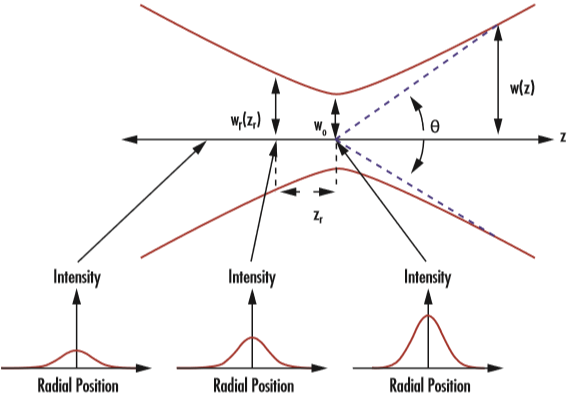
Figure 2 : Les faisceaux gaussiens sont définis par leur waist de faisceau (w0), leur longueur de Rayleigh (zR), et leur angle de divergence (θ)
La variation du diamètre du faisceau dans la région du waist du faisceau est définie comme suit :
La longueur de Rayleigh d'un faisceau gaussien est définie comme étant la valeur de z où l'aire de la section transversale du faisceau est doublée. Cela se produit lorsque w(z) a augmenté pour atteindre √2 w0. À l'aide de l'équation 4, la longueur de Rayleigh (zR) peut s'exprimer comme suit:
Cela permet également de lier w(z) à zR:
Le front d'onde du laser est plan au niveau du waist du faisceau et s'approche à nouveau de cette forme à mesure que la distance augmente par rapport à la région du waist du faisceau. Cela se produit car le rayon de courbure du front d'onde commence à se rapprocher de l'infini. Le rayon de courbure du front d'onde décroît par rapport à l'infini au niveau du waist du faisceau pour atteindre une valeur minimale au niveau de la longueur de Rayleigh, puis se rapproche à nouveau de l'infini lorsqu'il est éloigné du laser (Figure 3); ceci est vrai des deux côtés du waist du faisceau.3
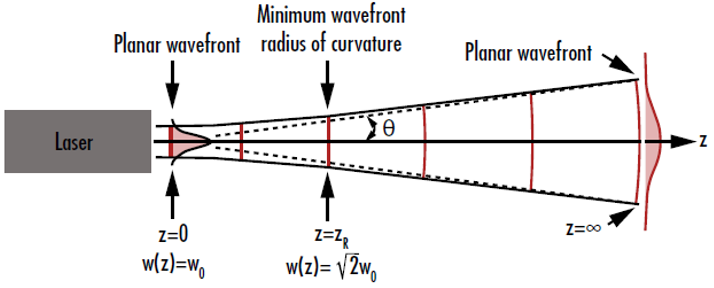
Figure 3 : La courbure du front d'onde d'un faisceau gaussien est proche de zéro lorsqu'elle est à la fois très proche et très éloignée du waist du faisceau
Manipulation d'un faisceau gaussien
De nombreux systèmes d'optique laser nécessitent la manipulation d'un faisceau gaussien et n'utilisent pas un simple faisceau « brut ». Pour ce faire, des composants optiques, tels que des lentilles, des miroirs, des prismes, etc., peuvent être utilisés. Vous trouverez ci-dessous un guide concernant les manipulations les plus courantes des faisceaux gaussiens.
Équation des lentilles minces pour les faisceaux gaussiens
Le comportement d'une lentille mince idéale peut être décrit au moyen de l'équation suivante2:
Dans l' équation 7, s’ est la distance entre la lentille et l'image, s la distance entre la lentille et l'objet et f la distance focale de la lentille. Si l'objet et l'image sont à des côtés opposés de la lentille, s est une valeur négative et s’ une valeur positive. Cette équation ignore l'épaisseur d'une lentille réelle et n'offre par conséquent qu'une simple approximation d'un comportement réel (Figure 4). L'équation des lentilles minces peut également s'écrire sans dimension en multipliant les deux côtés de l'équation par f:
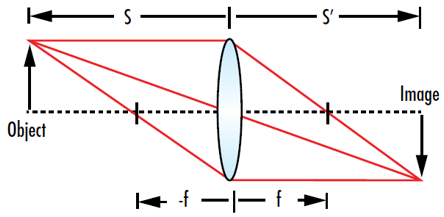
Figure 4 : L'équation des lentilles minces permet de déterminer la position d'une image (s’) lorsque la distance entre la lentille et l'objet (s) et la distance focale de la lentille (f) sont connues
En plus de décrire des applications d'imagerie, l'équation des lentilles minces peut s'appliquer à la focalisation d'un faisceau gaussien en traitant le waist du faisceau d'entrée en tant qu'objet et le waist du faisceau de sortie en tant qu'image. Les faisceaux gaussiens restent gaussiens après avoir traversé une lentille idéale sans aucune aberration. En 1983, Sidney Self a développé une version de l'équation des lentilles minces prenant en compte la propagation gaussienne4:
La distance totale entre le laser et le spot focalisé est calculée en ajoutant la valeur absolue de s à s’. L'équation 9 9 peut également s'écrire sans dimension en multipliant les deux côtés par f :
Cette équation s'approche de l'équation des lentilles minces standard à mesure que zR/f as'approche de 0, ce qui permet l'utilisation de l'équation des lentilles minces standard pour les lentilles à distance focale longue. Les équations 9 et 10 peuvent être utilisées pour trouver l'emplacement du waist du faisceau après l'imagerie à travers la lentille (Figure 5).

Figure 5 : Lors de la refocalisation d'un faisceau gaussien, « l'objet » est le waist d'entrée et « l'image » est le waist de sortie
Une courbe de la distance de l'image normalisée (s’/f) par rapport à la distance de l'objet normalisée (s/f) indique les emplacements de waist de sortie possibles à une longueur de Rayleigh normalisée donnée (zR/f) (Figure 6). Cette courbe indique que les faisceaux gaussiens focalisés à travers une lentille présentent quelques différences clés par rapport à l'imagerie à lentille mince traditionnelle. L'imagerie de faisceau gaussien présente à la fois une distance d'image possible minimale et une distance d'image possible maximale, contrairement à l'imagerie à lentille mince traditionnelle. La distance d'image maximale d'un faisceau gaussien refocalisé se produit avec une distance d'objet de -(f + zR), et non de –f. Le point de la courbe où s/f est égal à -1 et s’/f est égal à 1 indique que le waist de sortie se trouvera au niveau du point focal arrière de la lentille si l'entrée est au niveau du point focal avant d'une lentille positive.
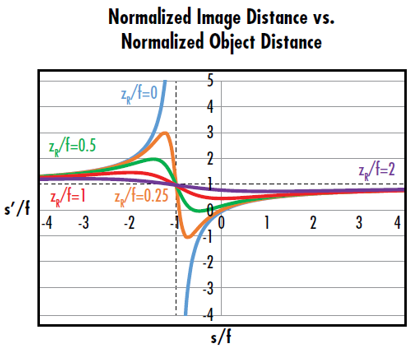
Figure 6 : La courbe avec zR/f=0 ccorrespond à l'équation des lentilles minces traditionnelles. Les courbes avec zR/f>0 indiquent que l'imagerie gaussienne présente des distances d'image minimale et maximale définies par la longueur de Rayleigh
Afin de comprendre le waist du faisceau et la longueur de Rayleigh après que le faisceau a traversé la lentille, il est nécessaire de connaître le grossissement du système (α), donné par :
Où w0 est le waist du faisceau avant la lentille et w0’ est le waist du faisceau après la lentille. L'équation des lentilles minces pour les faisceaux gaussiens peut ensuite être réécrite de manière à inclure la longueur de Rayleigh du faisceau après la lentille (zR'):
L'équation ci-dessus va s'effondre si la lentille est au niveau du waist du faisceau (s=0). L'inverse de la constante de grossissement au carré peut être utilisé pour relier les tailles de waist du faisceau et leurs emplacements3:
Focalisation d'un faisceau gaussien en spot
Dans de nombreuses applications, telles que le traitement des matériaux par laser ou la chirurgie, il est très important de focaliser un faisceau laser de manière à obtenir un spot aussi petit que possible afin de maximiser l'intensité et de minimiser la zone chauffée. Dans de tels cas, le but est de minimiser w0' (Figure 7). Une version modifiée de l'équation 13 peut être utilisée pour savoir comment minimiser le waist du faisceau de sortie3:
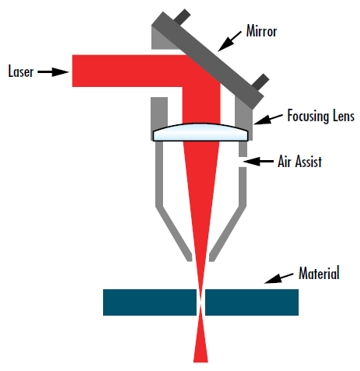
Figure 7 : Focaliser un faisceau laser pour obtenir la plus petite taille possible est crucial dans de nombreuses applications, y compris cette installation de découpe laser
Après multiplication des deux côtés par le dénominateur du côté gauche de l'équation puis multiplication des deux côtés par (w0')2, l'équation 14 devient:
La résolution de w0' donne :
Le waist du faisceau focalisé peut être minimisé en réduisant la distance focale de la lentille et |s|-f. Les termes à côté de w0 dans l'équation 17 sont définis comme étant une autre forme de la constante de grossissement α afin de comparer les valeurs du faisceau d'entrée à celles du faisceau de sortie une fois la lentille traversée (Figure 8).3
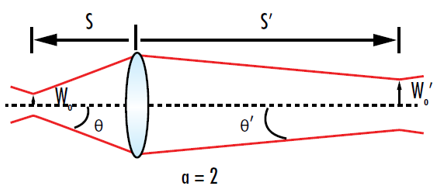
Figure 8 : Pour un grossissement de 2, le waist du faisceau de sortie sera le double du waist du faisceau d'entrée et la divergence de sortie sera deux fois moindre que la divergence du faisceau d'entrée
Il existe deux cas limite simplifiant davantage les calculs de la taille du waist du faisceau de sortie et son emplacement : lorsque s est largement inférieur à zR ou largement supérieur à zR.3 Lorsque la lentille se trouve bien dans la longueur de Rayleigh du laser, s << zR and (|s| − f)2 < zR2. L'équation 18 se simplifie pour donner :
Cela simplifie également les calculs pour le waist du faisceau de sortie, sa divergence, sa longueur de Rayleigh, ainsi que l'emplacement du waist :
Lorsque s >> zR, la distance entre la lentille et le spot focalisé est égale à la distance focale de la lentille.
L'autre cas limite se rencontre quand la lentille est largement en dehors de la longueur de Rayleigh et s >> zR, ce qui simplifie l'équation 18 pour donner :
Le diamètre du waist du faisceau de sortie est ainsi :
Comme lorsque s << zR, les calculs pour le waist du faisceau de sortie, la divergence, la longueur de Rayleigh et l'emplacement du waist du faisceau sont aussi simplifiés :
Lorsque s >> zR, la distance entre la lentille et le spot focalisé est égale à la distance focale de la lentille.
Ces deux résultats sont intuitivement logiques car le front d'onde du faisceau est approximativement plan, autant au niveau du waist du faisceau qu'à une distance très éloignée de celui-ci. À ces emplacements, le faisceau est presque parfaitement collimaté (Figure 9). Selon l'équation des lentilles minces standard, une entrée collimatée présente une distance d'image égale à la distance focale de la lentille.

Figure 9 : Le spot focalisé d'un faisceau gaussien après qu'il a traversé une lentille se trouvera au niveau du point focal de la lentille si le waist du faisceau d'entrée est soit très proche, soit très éloigné de la lentille. Cela est dû au fait que le faisceau d'entrée est approximativement collimaté à ces points
Décalage focal gaussien
De manière contre-intuitive, l'intensité d'un faisceau focalisé en une cible à une distance fixe (L) de la lentille n'est pas maximisée lorsque le waist se trouve au niveau de la cible. L'intensité sur la cible est en fait maximisée lorsque le waist a lieu à un point situé avant la cible (Figure 10). Ce phénomène est connu sous le nom de décalage focal gaussien.
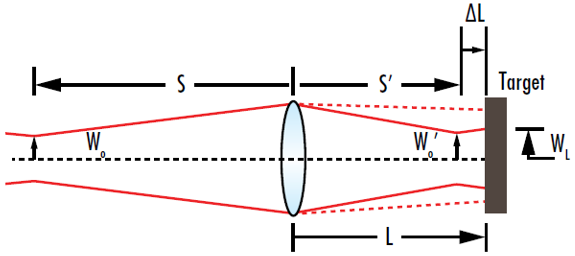
Figure 10 : Le rayon de faisceau minimal au niveau d'une cible a lieu lorsque le waist du faisceau focalisé se trouve à un endroit spécifique avant la cible, et non lorsque le waist focalisé se situe au niveau de la cible
La présente note d’application ne couvre pas la longue déduction, mais le rayon du faisceau au niveau de la cible peut être décrit par l'expression suivante4:
La différenciation de l'équation 34 par rapport à la distance focale de la lentille de focalisation (f) et la résolution de f lorsque d⁄df [wL (f )] = 0 révèle la distance focale de la lentille entraînant le rayon de faisceau minimal, et par conséquent l'intensité la plus élevée, au niveau de la cible.
À mesure que |s| se rapproche de zéro ou de l'infini, d⁄df [wL (f )] = 0 lorsque f = L. Dans ces deux cas, le faisceau d'entrée est approximativement collimaté ; il s'en suit donc que le plus petit rayon du faisceau a lieu au point focal de la lentille.
Collimation d'un faisceau gaussien
L'obtention d'un faisceau parfaitement collimaté avec une divergence de 0 est impossible, mais il est possible d'obtenir un faisceau approximativement collimaté soit en minimisant la divergence ou en maximisant la distance entre le point d'observation et le waist du faisceau le plus proche. Comme la divergence d'entrée est inversement proportionnelle à la constante de grossissement α, la divergence de sortie atteint une valeur minimale lorsque |s| = f (Figure 11).
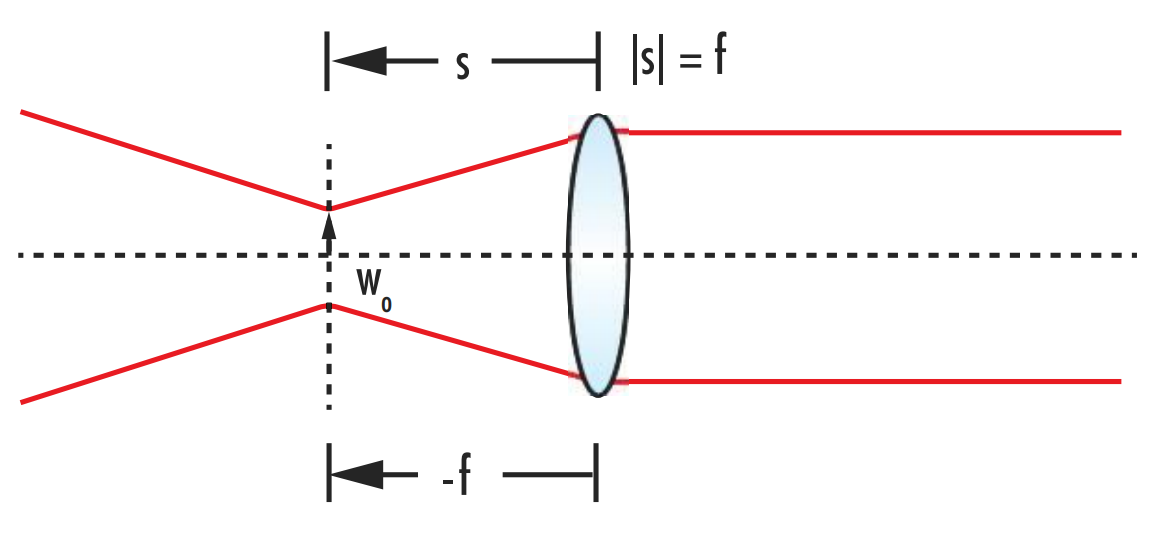
Figure 11 : Pour collimater un faisceau gaussien, la distance entre le waist du faisceau et la lentille de collimation doit être égale à la distance focale de la lentilleh
References
- Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
- Self, Sidney A. “Focusing of Spherical Gaussian Beams.” Applied Optics, vol. 22, no. 5, January 1983.
- O'Shea, Donald C. Elements of Modern Optical Design. Wiley, 1985.
- Self, Sidney A. “Focusing of Spherical Gaussian Beams.” Applied Optics, vol. 22, no. 5, Jan. 1983.
- Katz, Joseph, and Yajun Li. “Optimum Focusing of Gaussian Laser Beams: Beam Waist Shift in Spot Size Minimization.” Optical Engineering, vol. 33, no. 4, Apr. 1994, pp. 1152–1155., doi:10.1117/12.158232.
More Resources













 Section précédente
Section précédente 


























































ou consulter les numéros d’autres pays
facile à utiliser
entrer les numéros de stock pour commencer
Copyright 2023 | Edmund Optics SARL, 76-78 rue d’Alsace, 69100 Villeurbanne, France
L'entreprise Edmund Optics GmbH en Allemagne agit comme un mandataire d'Edmund Optics Ltd au Royaume-Uni. Le titulaire du contrat est Edmund Optics Ltd au Royaume-Uni.